데이터분석 4: 머신러닝 분석 방법론 pt. 2

선형 판별분석과 이차 판별분석(분류 모델)

판별분석이란?

• 로지스틱 회귀분석처럼 질적 척도로 이루어진 종속변수를 분류할 때 쓰이는 분석 기법이다
  • 기계학습보다는 통계기반의 데이터 분류 모델에 더 가깝다
• 회귀 분석처럼 최소 제곱법을 사용하는 처정방법을 통하여 독립변수의 최적 가중치를 구한다
• 독립 변수들이 정규분포를 따르지 않더라도 활용이 가능한 모델이다
• 일반 판별분석 (혹은 두 집단 판별분석): 종속변수의 범주가 2개일 경우
• 다중 판별분석: 범주가 3개 이상을 경우
• 범주를 구분하는 결정경계선을 산출하는 방식에 따라 → 선형 판별 분석 or 이차 판별분석으로 구분된다

선형 판별분석

• 분류 모델뿐만 아니라 PCA와 같은 차원축소에도 사용된다
• PCA와의 가장 큰 차이 → 종속변수를 사용하는 지도학습으로 차원 축소를 한다 → PCA보다 차원축소 성능이 우수하다
• 종속변수의 범주 간 분별 정보를 최대한 유지시키면서 차원을 축소시키는 방식으로 데이터의 오분류율이 최소가 되는 축을 찾는
• 선형 판별함수를 사용한다 → 전체 범주의 분류 오차를 최소화하는 것 → 도출한 다음 모든 관측치의 분류점수를 도출한다
• 분류점수: 해당 관측치가 어느 범주에 속할 것인지를 예측할 수 있는 것
• 집단 내 분산에 비해 집단 간 분산의 차이를 최대화하는 독립변수의 함수를 찾는 것
• 판별점수를 구하는 방법은: 판별상수를 더해준다 → 각 독립변수의 값에 판별계수를 곱한 값을 모두 더해준다
  • 각 범주에 대한 선형 판별함수가 도출되며, 관측치에 대하여 범주별 분류점수를 계산 → 가장 큰 분류점수를 갖는 범주로 관측치를 분류해 준다.
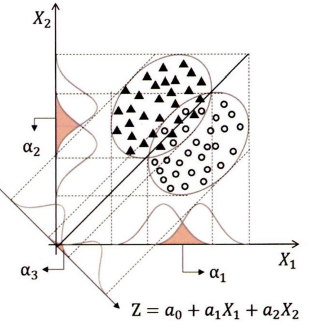
    • $Z = a_0 +a_1X_1+a_2X_2+…+a_kX_k$
• 충족되어야 하는 조건:
  1. 데이터가 정규 분포한다
  2. 각각의 범주들은 동일한 공부산 행렬을 갖는다
  3. 독립변수들은 통계적으로 상호 독립적이다 → 충족하지 않으면 이차 판별분석 사용
     • 실무 데이터에서 위 조건들이 완벽히 충족되지 않는 경우 많다 → 데이터 전처리

• 최적의 분류선인 결정경계선을 찾아내는 것이 판별분석의 핵심 로직이다

  

  • 위 크림과 같이 두 집단을 가장 잘 나눠줄 수 있는 직선을 만들어 주는 것이 선형 판별함수의 개념이다
  • 두 집단의 오분류 크기를 최소화하기 위하여 분류선의 각도를 정해주는 함수 z를 만드는 것

• 최적의 각도를 찾는 원리:

  

  • 독립변수 $X_1$만으로 두 집단을 분류할 경우 → 오분류의 크기는 $\alpha_1$이 된다.
  • $X_2$만으로 분류할 경우 → 오분류의 크기는 $\alpha_2$가 된다.
  • $X_1$과 $X_2$ 두 변수를 사용하게 되면 → 각 변수에 각도를 조정할 수 있는 계숫값을 조정해 주면서 최적의 일차 방정식을 도출
  • 오분류 크기 $\alpha$가 최소화되는 직선의 함수식이 완성되면 → 각 관측치의 변숫값을 대입하여 분류점수를 구할 수 있다.
• 독립변수들 간의 조합을 통해 최적의 분류식을 만드는 방식 → 모든 독립변수를 다 넣는 것보다는 분류에 유의미한 변수를 선택하여 모델을 만드는 것이 좋다.
• 같이 변수선택방법을 사용하여 모델의 성능을 향상시킬 수 있다.
• 고윳값을 이용하여 판별분석 모델의 설명력에 대해 평가할 수 있다.
  • 고윳값이 크다 → 집단 간 차이 크다 → 설명력이 높다고 해석
    • 4.0 이상이면 판별 모델로서 설명력이 있다고 판단

이차 판별분석

• 선형 판별분석이 공분산 구조가 많이 다른 범주의 데이터를 잘 분류하지 못한다는 단점을 보완한 방법 → 범주 간의 공분산 구조가 다를 때는 사용
• 비선형 분류가 가능하다는 장점 있지만 독립변수가 많을 경우 추정해야 하는 모수가 많아져서 선형 판별분석에 비해 연산량이 큰 단점이 있다
• 기본적인 원리: 선형 판별분석과 유사하지만 변수에 제곱을 취한 추가적인 변수들을 사용하여 결정경계선을 곡선의 형태로 만들어준다
  • 오분류 기대비용 (ECM: Expected Cost of Misclassification)

    • $\text{ECM} = C(1

      2)P(1

      2)P_1+C(2

      1)\times P(2

      1)(P_2)$

    • 최소화할 때 최적의 C지점을 찾을 수 있으므로 이 공식에 의하면 각 범주에 분류하는 방식은 다음과 같다

      

      • \[\begin{aligned} \frac{f_1(x)}{f_2(x)} \geq \frac{\pi_2}{\pi_1} \times \frac{C(1|2)}{C(2|1)} : x\text{를 1번 범주로 분류}\\ \frac{f_1(x)}{f_2(x)} < \frac{\pi_2}{\pi_1} \times \frac{C(1|2)}{C(2|1)}:x\text{를 2번 범주로 분류} \end{aligned}\]
• 오분류 비용과 각 범주의 분산 차이를 고려하여 이차식으로 결정경계선을 산출

  • $\delta_k(x) = -\frac{1}{2}\log{

    \sum{k}

    } - \frac{1}{2}(x-\micro_k)^T\sum_K^{-1}(x-\micro_k)+\log{\pi_k}$

서포트벡터머신(SVM; 분류 모델)

• 판별분석과 같이 범주를 나눠줄 수 있는 최적의 구분선(결정경계선)을 찾아내어 관측치의 범주를 예측해주는 역사 깊은 모델
• 이진 분류에만 사용 가능하다는 단점이 있지만, 로지스틱 회귀나 판별분석에 비해 비선형 데이터에서 높은 정확도를 보이며 다른 모델들보다 과적합 되는 경향이 적다 → 인기가 많은 분석 방법
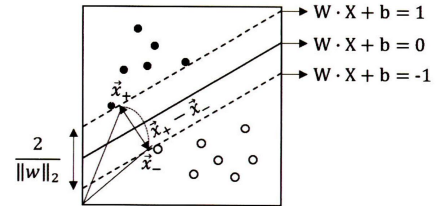
• 결정경계선의 양쪽의 마진(Margin: 빈 공간)을 최대하도록 만들어지는 것
• 서포트 벡터란: 샘플수가 마진과 맞닿아서 결정경계선의 위치와 각도를 정해줄 수 있는 기준이 되는 관측치 → SVM은 서포트벡터만으로 범주의 구분 기준인 결정경계선을 정해서 학습 효율이 높다
  • 따라서 → 마진이란: 결정경계선과 서포트 벡터와의 거리

  

• 변수마다 스케일이 다르게 되면 모델 성능이 매우 떨어지게 되는 것 → 기계학습에서 거리를 통해 분류나 회귀 모델을 만들 때는 반드시 데이터 정규화나 표준화를 해주어야 한다
• 최적 결정경계선을 찾기 위해서는 독립변수가 k개라 하면 최소 K+1개의 서포트벡터가 필요
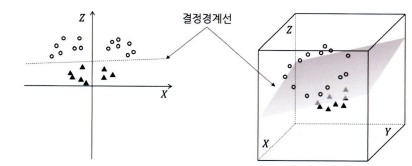
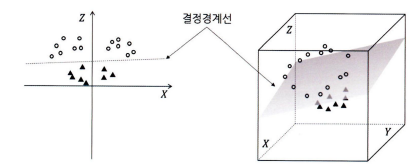
  • 독립변수 2개인 2차원상 → 결정경계선
  • 독립변수 3개로 늘어나는 경우 → 평면
  • 그 이상으로 차원이 증가하는 경우 → 초평면(hyperplane) → 그림으로 표현할 수 없다
    • Maximum Marginal Hyperplane(MMH: 최대 마진 초평면)을 찾아 범주를 분리하는 분류 방법이라 할 수 있다
• 결정경계선 방식: $W \cdot X + b = 0$
  • $W$: 가중치 벡터
    • $W = {w_1, w_2, …, w_k}$
  • $X$: 각 독립변수
  • $b$: 편항값(bias)
  • 값은 0이라서 경계선 위에 관측치는 0보다 크고 아래에 있는 0보다 작다
    • 결정계선 위의 관측치: $W \cdot X+b=w_0+w_1x_1+w_2x_2+…+w_kx_k>0$
    • 결정계선 아래의 관측치: $W\cdot X+b=w_0+w_1x_1+w_2x_2+…+w_kx_k<0$
    • 이를 응용하여 서포트 벡터들과 맞닿은 위아래 마진의 값을 $1$과 $-1$로 정의하면 각 관측치의 값: $w_0+w_1x_1+w_2x_2+…+w_kx_k\geq \pm{1}$
• 결정경계선으로부터 마진까지의 거리는 유클리드 거리를 통해 구할 수 있다
  • 마진의 거리: $\left\Vert x^+ - x^- \right\Vert$ → $\frac{2}{\sqrt{w^T\cdot w}} = \frac{2}{\left\Vert w \right\Vert_2}$가 된다 \(\begin{aligned} & \text{Margin} = \text{distance}(x^+, x^2) \\ & = \left\Vert x^+ - x^ - \right\Vert_2 \\ & = \left\Vert (x^- + \lambda w) - x^- \right\Vert_2 \\ & = \left\Vert \lambda w \right\Vert_2 \\ & =lambda\sqrt{w^T \cdot w}\text{, } \left(\lambda = \frac{2}{w^T\cdot w}\right) \\ & = \frac{2}{w^T \cdot w}\cdot \sqrt{w^T\cdot w} \\ & = \frac{2}{\sqrt{w^T\cdot w}} = \frac{2}{\left\Vert w \right\Vert}\end{aligned}\)
• 대부분 데이터는 이상치가 있기 마련이다 → 이상치를 허용하지 않는 경우 과적합 문제가 발생 가능 → 어느 정도 이상치를 허용해 주도록 해줄 필요가 있다 → Soft Margin(소프트 마진): 마진을 최대화하여 과적합을 방지해 주는 것
  • Hard Margin(하드 마진): 이상치를 허용하지 않는 것
  • 파이썬에서 C와 Gamma 매개변수를 이용하여 조정해줄 수 있다
    • C값을 낮게 설정하면 이상치들이 있을 가능성을 높게 잡는다
    • Gamma: 하나의 관측치가 영향력을 행사하는 거리를 조정해 주는 것 → 값이 클수록 영향력의 거리는 짧아지게 된다
  • 이상치 상태가 더 극단적으로 이루어진 데이터 → Kernel trick(커널 기법): 기준의 데이터를 고차원 공간으로 확장하여 새로운 결정경계선을 만들어내는 방법
    • Gamma 매개변수로 조정 → Gamma값은 커질수록 각각의 관측치에 대한 결정경계선 범위가 작아져서 결국 여러 개의 결정경계선이 생기게 된다
    • 

KNN(분류, 예측 모델)

• 쉽고 직관적인 분류모델로 알려져 있지만 의사결정나무처럼 연속형 종속변수의 회귀예측도 가능한 모델이다
• 학습 데이터의 별도 학습 과정이 없다 → 미지 저장되어 있는 학습 데이터에다가 예측 데이터를 대조함으로써 직접 결과가 도출되므로 메모리 기반 학습(Memory-based learning)이라고도 함
  • 공간상에 이웃해 있는 관측치의 범주나 값을 통해 결과를 출력
• 독립변수들의 값이 비숫하면 범주도 같다는 심플한 사상으로 시작한 모델이다
• 하나의 근접한 학습 데이터로 분류를 하는 것은 1NN 모델임 → K는 양의 정수로 다양하게 세팅할 수 있다 → 통상적으로는 10 이하로 맞춰줌
• 데이터의 지역 구조(local structure)에 민감한 특성을 가지고 있다 → 근접한 과반수의 범주를 따르다 보니 범주의 분포가 편향되어 있을 경우에는 예측 데이터의 관측치들이 빈도 높은 범주로 강하게 쏠리는 단점이 있다 → K를 잘 설정해야 된다
  • 동률의 범주가 생겨 분류를 할 수 없는 상황을 방지하기 위하여 이진 분류의 경우 홀수의 K를 설정하는 것이 좋다
    • K가 너무 크면 전체 범주의 분포의 영향을 많이 받게 되고 관련이 적은 먼 곳의 데이터가 분류에 영향을 미치게 된다
    • K가 너무 작으면 이상치의 영향을 많이 받고 패턴이 직관적이지 못한

K를 선택하는 방법

• 교차검증(cross validation)을 하여 오분류율이 가장 낮아지는 K수를 탑색
  • K 수를 1부터 계석 늘려가며 검증 데이터의 오분류율이 어떻게 변화하는지 관찰 → 특정 지점에서 오분류율이 최저점을 찍고 다시 높아진다
  • 오분류율이 가장 낮았던 지점의 K 수를 선정하면 된다
  • 보다 정확한 K 탐색을 위하여 교차검증을 여러 번 수행하는 K-fold 교차검증을 하기도 한다

가중치

• 멀리 있는 관측치는 영향력을 적게 받도록 하기 위해 거리에 가중치를 줄 수 있다
• 3 가지 방법:
  1. d가 이웃 관측치까지의 거리일 때 관측치에 거리의 역수 $\frac{1}{d}$를 가중치로 하는 것 → 가장 흔한 방법 → 근접한 이웃들 간에 가중치 값이 큰 차이를 나타내도록 조정해 준다
  2. $\frac{1}{1+d^2}$ → 근접한 이웃들의 관측치들은 가중치 값이 비슷하게 유지되다가 거리가 멀어지면 영향력을 확연히 떨어지도록 조정해 준다.
  3. $e^{-d}$
     • 어떤 가중치가 더 효과적인지는 데이터의 상황에 따라 다르다 → 가중치도 교차검증을 통해 최적의 알고리즘을 선택해야 된다

거리 계산

• 유클리드 거리
  • $d(X,Y) =\sqrt{(x_1-y_1)^2 +(x_2-y_2)^2+…+(x_n-y_n)^2}$
• 거리를 사용해서 데이터 정규화나 표준화를 반드시 해줘야 한다 → 명목형 독립변수의 경우에는 0과 1로 더미 변수 처리를 하여 사용

KNN 회귀

• 종속변수가 연속형 변수인 경우에 사용 → 원리는 분류 모델과 동일한다
• 이웃한 K개 관측치의 평균값을 계산하면 된다
• K를 너무 적개 설정하면 학습 데이터에 너무 의좀된 모델이 되어 일반화가 어려워진다 → 안정된 예측 모델을 만들기 위해서는 학습 데이터셋에서 정확도가 다소 떨어지더라도 K를 3이상으로 설정해주는 것이 좋다

장단점

• 정점:
  • 쉽고 직관적이다
• 단점:
  • 변수가 100개 이상으로 많아지거나, 데이터 양이 커지게 되면 연산량 증가가 다른 모델보다 훨씬 크기 때문에 다소 비효율적이다 → 대량의 데이터를 다루는 분석 프로젝트에는 적절하지 않은 모델이라 할 수 있다
  • 분류 모델에서 특정 하나의 범주가 대부분을 차지하고 있는 상황에서는 분류가 잘되지 않는다

시계열 분석(예측 모델)

• 관측치의 통계량 변화를 시간의 흐름에 따라 순차적(Sequential)으로 데이터화하고 현황을 모니터링하거나 미래의 수치를 예측하는 분석 방법이다
• 목적:
  1. 탐색 목적: 외부 인지와 관련된 계적적인 패턴, 추세 등을 설명하고 인과관례를 규명한다
  2. 예측 목적: 과거 데이터 패턴을 통해 미래의 값을 예측한다
• 한 시점의 관측결과는 $X$는 시간 $t$에 따라 변동하는 값이므로 $X_t$로 나타낸다
  • $X_t = S_t\text{(신호)}+a_t\text{(잡음)}$
  • 신호와 잡음의 개념 → 수준, 추세, 순환성, 계절성, 잡음으로 나눌 수 있다 → 시계열 분해
    • 수준(Level): 시계열의 평균값
    • 추세(Trend): 장기 변동 요인으로써 강한 외부요인이 없는 한 지속도는 경향성
    • 순환성(Cycle): 불규칙적이며 빈복적인 중기 변동요인
    • 계절성(Seasonality): 1년(12개월)의 기간 동안의 주기적인 패턴
    • 잡음(Noise): 일정한 규칙성이 없는 무작위적인 변동 그래프로 표현을 하면:
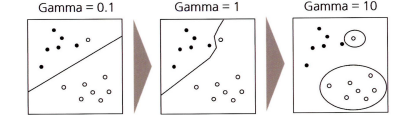
    • 추세와 순환성을 합쳐서 추세라고 표현하기도 한다
    • 시계열 분해를 통해 숨겨진 요소를 파악하고 분석을 진행해야 예측력을 높일 수 있다
    • 시계열 분해 방법: → 파이썬에서는 seasonal_decompose 라이브러리를 활용
      • Seasonal Extraction in ARIMA Time Series (SEATS) 분해 방법
      • Seasonal and Trend decomposition using Loess (STL) 방법
• 시계열 분석 방법:
  • 회귀 기반 방법
  • ARIMA 모델
  • 지수평활법

    회귀 기반 시계열 분석

• 예측하고자 하는 $t$의 값이 종속변수가 되고 $t$ 시점에 해당하는 요소(해당 요일, 월 등)들이 독립변수가 된다 → 요소의 변수는 실제로는 더미변수로 변환해야 모델을 학습시킬 수 있다
• $Y_t = \beta_0 + \beta_1X_1 +\beta_2X_2 + … + \beta_pX_tp+w_t$
  • 해당 시점에 대한 요소에 대한 정보를 독립변수화함으로써 시즌성이나 순환성을 모델에 반영할 수 있다
  • 점점 값이 증가하거나 감소하는 추세성을 반영하려면 → 시계열이 시작하는 기준 시점일로부터의 경과일을 독립변수화하면 된다.
• 비선형적인 경우에는 일반 선형 회귀식우로 표현하는 것이 어렵다 → 다항회귀
  • $Y_t = \beta_0 + \beta_1X_1 + \beta_2X_2^2 + w_t$
  • 또는 종속변수나 독립변수에 로그를 취해주어 비선형적 관계를 적합시킬 수 있다 → 모든 관측치 값이 0보다 커야 한다 ->만약 변수에 0이 포함되어 있는 경우에는 $\log{(x+1)}$과 같은 변환을 해줘야 한다.
    • 종속변수를 로그변환 해주었을 때는 다른 일반 선형 모델과 비교하고나 예측값을 해석할 때 역산하여 기준을 맞춰야 한다.
    • 과적합 위험이 있다 → 과도한 변수 변형은 모델의 예측력을 저하시킬 수 있으므로 주의해야 한다.
• 장점:
  • 외부 요소를 변수로 추가해 주는 것이 용이하다는 것이다
  • 영향을 줄 수 있는 외부 요소를 독립변수로 함께 넣을 수 있다
  • 전달 혹은 3달 전이라 전년도 동일 등에 대한 과거 기간의 수치를 독립변수로 넣어주면 추세 요소를 보다 정규하게 반영할 수 있다 → 자기회귀(Autoregression) 요소를 반영하는 개념으로써 시차 이동에 따른 수치 변화에 대한 설명력을 보다 높일 수 있다.
• 자기회귀 요소 변수는 점 달의 수치가 유의미할 수도 있고, 6개월 전, 12개월 점 등 유의미한 변수가 될 수 있는 경우의 수가 매우 많다 → 과거 시차 중 언제 시점이 종속변수의 수칭에 영향을 주는지 쉽게 확인하기 위한 자기상관함수 기법
• 자기상관함수인 Autocorrelation Function(ACF)를 이용하여 시계열 데이터의 주기성을 수치적으로 확인할 수 있도, 어떠한 특정 시차가 어떠한 영향으로 주는지 알 수 있다.
  • 자기상환함수로써 $Y$ 수치와 $t_0\sim t_{-k}$ 시점과의 상관관계를 0.05 유의수준 안에서 나타낸 것
  • 점선으로 되어있는 가로선을 벗어나면 해당 시차가 $Y$값과 상관성이 있다는 뜻 → 다소 주관적인 기준으로, 상황에 따라 살짝만 나온 지점은 무시하기도 한다
  • 선막대가 0보다 크다 → 양의 상관관계
  • 선막대가 0보다 작다 ->음의 상관관계
• 시계열 데이터에 추세가 존재할 경우 → 근접한 시차에 대한 상관성은 높은 양의 값을 갖게 되는 경향이 있다 → 추세가 있는 데이터의 경우 근접한 시차의 ACF값이 높은 양의 상관성을 갖는 것
• 편자기상관함수인 Partial Autocorrelation Function(PACF)-> $Y$의 시점과 특정 $t_{-k}$ 시점 이외의 모든 시점과의 영향력을 배제한 순수한 영향력을 나타내는 척도
  • 다른 시점들과의 다중공선성을 제거한 단 두 시점과의 관계를 수치화한 것
  • 시계열 분석을 할 때는 ACF와 FACF를 같이 봐야 한다
  • 두 기준은 AR, MA 등의 분석 방법에서 중요하게 사용된다
• 모델 학습과 해석, 예측 방법은 기존의 회귀분석과 동일

Autoregressive Integrated Moving Average (ARIMA) 모델

• 이동평균을 누적한 자기회귀를 활용하여 시계열 분석을 하는 것 → 자기회귀(AR) 모델과 이동평균(MA) 모델을 이해하고 있어야 ARIMA 모델을 알 수 있다
• AR, MA모형 분석을 시작하기에 앞서 시계열 데이터가 정상성(Stationarity)을 가지도록 변환을 해줘야 한다
  • 정상성이란: 모든 시점에 대해서 일정한 평균을 갖도록 하는 것 → 추세나 계절성이 없는 시계열 데이터로 만들어 주는 것
  • 주기의 고점이나 저점을 알 수 없고 고정된 길이 갖고 있지 않다 → 시계열 데이터의 주기성은 저상성과 관련 없다
  • 정상성을 나타내는 시계열은 평균과 분산이 안정되어 있는 상태
• 시계열 데이터에 추세가 있어서 평균이 일정치 않으면 차분(difference)을 해준다
  • 현재 상태의 값에서 바로 전 상태의 값을 빼 주는 것 → 모든 기간의 평균을 일정하게 해 준다
  • 추세만 차분하는 것은 1차 차분 혹은 일반 차분이라 한다
  • 시계열에 계절성도 존재하는 경우에는 계절성의 시차인 $n$ 시점 전 값을 빼 주는 2차 차분 혹은 계절차분을 해준다.
• 시계열 데이터의 분산이 일정치 않을 때는 변환을 해주어야 한다
  • 분산이 점점 커져가는 형태를 가지는 경우 각 시점의 값에 로그나 루트를 씌워 주어 분산의 크기를 완화시켜 주는 것
  • 분산을 없애 주지는 못하지만 시점 간의 편차를 감시키기 때문에 시계열 분석에서 유용하게 사용된다

    자기회귀

• 자신에 대한 변수의 회귀라는 뜻
• 현재 시점의 $Y$값과 $t_{-k}$ 시차들 간의 관계만으로 시계열 데이터를 분석하는 것
• 시차 변수만 사용한 개념
• $\text{AR}(1): Y_t = \beta_1X_{t-n} + w_t$
  • $Y_t$ 갑은 $X_{t-n} 시점의 값에 자기상관관계수 $\beta_{t-n}$값을 곱하고 오차 항 $w_{t-n}$를 더해주는 식으로 구성

이동평균

• 관측값의 이전 시점의 연속적인 예측 오차의 영향을 이용하는 방법
• $\text{MA}(1): Y_t = \epsilon_t + \beta_1X_{t-n}$
  • $Y_t$값은 해당 시점의 오차 항(백색자음) $\epsilon_t$에 n시점 이전의 오파항에 이동 평균계수를 곱한 값들을 더해 준 것
• 이전 시점의 상태를 이용하여 현재를 예측하는 방식이 아님
• 이전 시점의 변동 값과 오차항을 이용하여 현재 상태 추론

ARIMA

• AR 모델과 MA 모델은 각각 사용하는 시점의 수에 따라 AR(p), MA(q) 모형으로 정의할 수 있다.
  • 결합 → 자기회귀평균 모델 ARMA(p, q) 모델이 된다
  • 과거 시점의 수치와 변동성을 모두 활용하여 보다 정교한 예측을 하는 것
  • 보통 시계열 데이터는 추세를 가지고 있으며 일정한 패턴을 가지고 있지 않은 경우가 많다
  • 대부분 불안정한 퍁턴을 가지고 있기 때문에 ARMA(p, q) 모델만으로는 부족한 면이 있다
    • 불안정성을 제거하는 기법을 결합한 모델 → ARIMA 모델
• 과거의 데이터가 가지고 있던 추세까지 반영
• 시계열의 비정상성을 설명하기 위해 시점 간의 차분을 사용하는 것
• AR 모델의 자기 회귀 분석 차수, MA 모델의 이동평균 부분의 차수, 1차 차분이 포함된 정도를 포함하여 ARIMA(p, d, q)로 표현
• 시계열 데이터를 d회 차분하고 p만큼의 과거 값들과 q만큼의 과거 오차 값들을 통해 수치를 예측하고 차분한 값을 다시 원래의 값으로 환산하여 최종 예측삾을 산출
• 시각화와 ACF차트를 통해 시계열 데이터가 정상시계열인지 확인
  • 시계열 데이터에 추세가 있어서 평균이 일정치 않으면 차분을 하여 차분계수 d를 구한다 → ACF, PACF 값을 통해 p값과 q값을 설정하고 최종의 ARIMA(p, d, q)를 적합하여 모델을 만든다
• 시계열 분석의 예측값에 대한 평가는 실젯값과 예측값의 차이를 측정하여 모델의 적합도와 예측력을 평가한다 → RMSE, MAE, MAPE 등의 기준을 사용
• 시계열 데이터는 검증할 데이터가 적은 편이다 → 슬라이딩 윈도우 기법을 사용하여 학습 및 검증 데이터를 증폭시킬 수 있다
  • 슬라이딩 윈도우 방식으로 시점을 중복하여 복제하면 시계열 전체 구간을 학습과 예측으로 사용하여 보다 정밀한 모델 검증 및 평가가 가능

K-Means 클러스터링(군집 모델)

• 비지도학습 → 미리 가지고 있는 정답(레이블) 없이 데이터의 특성과 구조를 발견해 내는 방식
• K는 분류할 군집의 수를 뜻한다
• Means: 각 군집의 중심(Centroid)을 뜻한다
• 중심점과 군집 내 관측치 간의 거리를 비용함수로 하여, 이 함수 값이 최소화되도록 중심점과 군집을 반복적으로 재정의해 준다 → K개의 중심점을 찍어서 관측치들 간의 거리를 최적화하여 군집화를 한다 → 정규화나 표준화 필요
• 방법:
• 지역 최솟값 문제: 중심점과 군젭 내 관측치의 거리 합이 최소화됐을 때 클러스터링 알고리즘이 종료되기 때문에 정말로 거리합이 최고화되는 전역 최솟값을 찾기 전에 지역 최솟값에서 알고리즘이 종료되는 것 → 방지하기 위해 초기 중심점 선정 방법을 다양하게 하여 최족의 모델을 선정할 수 있다
  • 초기 중심점 선정 방법: 랜덤 방식, 중심점들을 가능한 한 서로 멀리 떨어져서 선정하는 방법, 중심점이 밀집되지 않도록 하는 K-Means++ 등
  • K의 수 선정하는 방법:
    1. 비즈니스 도메인 지식을 통한 개수 선정
    2. 엘보우 기반: 군집 내 중심점과 관측치 간 거리 합(Inertia value)이 급감하는 구간의 K 개수를 선정하는 방법
    3. 실루엣 계수(Silhouette Coefficient): 군집 안의 관측치들이 다른 군집과 비교해서 얼마나 비슷한지를 나타내는 수치 $S_i = \frac{b_i-a_i}{\text{max}(a_i, b_i)}$

연관구칙과 협업 필터링(추천 모델)

• 전통적으로 추천의 유형은 세 가지로 구분할 수 있다
• 추천 시스템 대표적인 방법:

연관 규칙

• A라는 제품을 구매한 사람은 B라는 제폼도 구매할 확률이 높다는 결과를 이끌어 내는 모델
• 대표적 알고리즘:
• 품목 간의 연관 관계 계산은 각 품목 조합의 출현 빈도를 이용
  • 조건 절(Antecedent): 상품 A를 구매한 사람은 B도 구매한다고 했을 때의 A를 구매한 현상
  • 결과 절(Consequent): B를 구매한 현상
• 세 가지 핵심 지표를 통해 품목 조합 간의 연관성의 수준을 도출:
  • 지지도: 전체 구매 횟수 중에서 해당 아이템 혹은 조합의 구매가 얼마나 발생하는지를 나타낸다
  • 신뢰도: 아이템(조합) A가 판매됐을 때 B 아이켐(조합)도 함께 포함되는 조건부 확률
    • P(A → B)와 P(B → A)는 다를 수 있다는 점을 주의
  • 향상도: 아이템 A의 판매 중 아이템 B가 포함된 비율이, 전체 거래 중 아이템 B가 판매된 비율보다 얼마나 증가했는지를 나타내는 지표
    • 두 아이템 간의 연관성을 나타내는 지표 → 조건절과 결과정의 위치가 바꾸어도 값이 동일한다
    • 대칭적 척도라고도 함
• 보완한 평가 척도
  • Interest-Support(IS) 측도: 향상도와 지지도를 함께 고려한 측도
    • 향상도와 지지도 중 하나가 너무 낮음에도 불규하고 연관규칙으로 선택되는 문제를 방지할 수 있다
  • 교차지지도: 전체 아이템 조합에서 어느 정도 수준의 지지도 이하를 버릴 것인가를 판단할 수 있는 하나의 보조지표
• Apriori 알고리즘: 지지도나 신뢰도가 낮을 조합은 처음부터 연산 대상에서 제외한다 → 의사결정나무의 pruning과 유사한 개념
  • 분석 순서:

콘텐츠 기반 필터링과 형업 필터링

콘텐츠 기반 필터링

• 아이템의 메타 정보를 활용하는 것
• 정형화된 데이터를 통해 기준의 선호와 유사한 아이템을 추천할 수 있다는 장점이 있다
  • 모든 제품에 대한 메타 정보를 입력해야 작동하기 때문에 아이템이 많아질 경우 관리가 힘들어지는 문제가 있다
  • 구매자가 선호를 표현한 아이템과 유사한 속성을 가진 아이템만 추천하기 때문에 속성이 유사하지 않더라도 구매할 가능성이 높은 제품을 추천할 수 없다는 단점이 있다
  • 해결 방법 → 협엽 필터링

협업 필터링

• 크기 최근점 이웃 모델과 잠재요인 모델로 구분되는 것
  • 최근접 이웃 방식은 사용자 기반과 아이템 기반 방식으로 구분된다
• 최근접 이웃 모델: 사용자들이 아이템에 매긴 평점 데이터를 기반으로 매기지 않은 아이템의 평점을 예측하는 방식으로 작동된다 → 예측한 평점이 높은 아이템을 추천해 주는 것
• 사용자 기반: 우사한 성향을 가진 사람들을 찾아내어 그 사람들이 선호하는 아이템을 추천해 주는 방식으로 수행된다 → 피어슨 유사도나 쿠사인 유사도를 통해 구할 수 있다
• 평점을 예측하고자 하는 방식:
• 아이템 기반: 사용자 기반과 유사하는데 관점만 사용자에서 아이템으로 바꾸어서 예측 점수를 도출
• 일반적으로 제품은 구매자들이 평점을 주는 경우가 드물다 → 희소 행렬 → 고객들의 구매이력을 사용
• 명시적 데이터: 호불호가 명확한 데이터
• 암묵적 데이터: 사용자의 호불호를 명확히 알 수 없는 데이터 → 이를 통한 모델은 잠재요인 모델임
• 잠재요인 모델: 사용자와 아이템 간의 관계 정보를 가지고 있는 데이터 행렬분해를 하여, 데이터 안에 숨겨져 있는 잠재 요인을 도출 → 일반적으로 20~100 가지 잠재 요인을 만든다
  • 행렬 분해를 위한 기본 기법은 특잇값 분해 → null 값으로 누락되어 있는 공간을 모두 평균값 등으로 대치 해줘야 한다