데이터 분석3-1: 통계 기반 분석 방법론 + 머신러닝 분석 방법론 pt. 1

분석 모델 개요

통계 모델이란?

• 모형과 해석을 중요하게 생각하며, 오차와 불확정성을 강조한다

  기계 학습이란?

• 대용량 데이터를 활용하여 예측의 정확도를 높이는 것을 중요하게 생각한다
• 통계 모델을 함께 활용하면 높은 성과를 얻어낼 수 있다.

  데이터 분석 방법론 개요

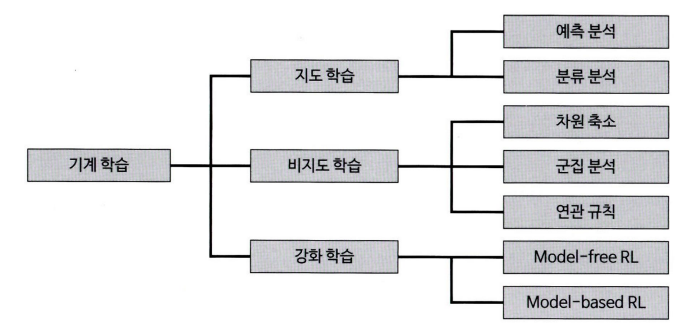
• 기계 학습 데이터 분석 방법론 2 가지 기준으로 구분할 수 있다
  1. 종속변수의 유무에 따라
     • 지도학습
     • 비지도학습
     • 강화학습
  2. 독립변수와 종속 변수의 속성에 따라 방법론 경정
     • 하나의 방법론이 양적, 질적 변수 형태에 모두 사용가능한 경우도 있다

구분	독립변수	종속변수	방법론	용도
통계모델	질적척도	질적척도	교차분석 스피어만 서열상관분석	연관성 분석
		양적척도	Z-test T-test	가설 검정
			ANOVA MANOVA	분산 분석
	양족척도	양족척도	피어슨 상관분석	연관성 분석
지도학습	질적척도	질적척도	로지스틱 회귀 분류 나무 랜덤포레스트 분류 나이브 베이즈 신경망	분류 분석
		양적척도	선형회귀 회귀 나무 랜덤포레스트 회귀 신경망	예측 분석
	양적척도	질적척도	로지스틱 회귀 분류나무 랜덤포레스트 분류 K-근접이웃 서포트 벡터 머신(SVM) 판별분석 신경망	분류 분석
		양적척도	선형회귀 회귀 나무 랜덤포레스트 회귀 K-근접이웃 신경망	예측 분석
비지도 학습	양적척도		주성분 분석 요인 분석	차원 축소
			K-Means Self-Organising Map (SOM)	군집 분석
	질적척도		Association Rule	연관 규칙
강화학습			Model-free RL
			Model-based RL

지도학습이란?

• 입력에 대한 정답이 주어져서 출력된 결괏값과 정답 사이의 오차가 줄어들도록 학습과 모델을 수정을 반복한다

  비지도학습이란?

• 자율학습이라고도 부름
• 별도의 정답이 없이 변수 간의 패턴을 파악하거나 데이터를 군집화하는 방법

  강화학습이란?

• 시행착오를 통해 학습하는 과정을 기본 콘셉트로 한 방법 중 하나이다

주성분 분석(PCA)

• 여러 개의 독립변수들을 잘 설명해 줄 수 있는 주된 성분을 추출하는 기법
  • 이를 통해 전체 변수들의 핵심 특성만 선별 → 독립변수(차원)의 수를 줄일 수 있다 → 차원의 저주를 방지
    • 여러 개의 변수들이 소수의 특정한 소수의 변수들로 축약되도록 가공하는 것
    • 차원 저주란?
      • 변수가 늘어남에 따라 차원이 커지면서 분석을 위한 최소한의 필요 데이터 건수가 늘어나면서 예측이 불안정해지는 문제
• 차원을 감소하는 방법:
  1. 변수 선택을 통해 비교적 불필요하거나 유의성이 낮은 변수를 제거하는 방법
  2. 변수들의 잠재적인 성분을 추출하여 차원을 줄이는 방법
• 데이터 공간에 위치하는 점들의 분산을 최대한 보존하는 축을 통해 차원을 축소하는 것이 핵심 요소이다
• 일반적으로 제1주성분, 제2주성분만으로 대부분의 설명력이 포함됨 → 2개의 주성분만 선정한다
• 주성분 찾는 방법: 데이터의 분산을 가장 잘 표현할 수 있는 저차원을 찾아내는 것

공통요인분석 (CFA)

요인분석 (Factor Analysis)

• 주어진 데이터의 요인을 분석한다는 큰 개념

탐색적 요인분석	확인적 요인분석
변수와 요인 간의 곤계가 사전에 정립되지 않을 때	이미 변수들의 속성을 예상하고 있는 상태에서 실제로 구조가 그러한지 확인하기 위해
체계화되지 않은 상태에서 변수 간의 관계를 알아보기 위해	보통 선행연구를 통해 밝혀진 변수의 속성을 활용하여 측정변수와 잠재변수 간의 관계를 검정 및 확인하기 위해

공통요인분석이란?

• 상관성이 높은 변수들을 묶어 잠재된 몇 개의 변수를 찾는다는 점에서 PCA와 차이가 있다

주성분 분석	공통요인분석
변수의 수를 축약하면서 정보의 손실을 최소화하고자 할 때 사용됨	변수들 사이에 존재하는 차원을 규명함으로써 변수들 간의 구조를 파악하는 데 주로 사용됨
모든 독립 변수들의 총 변량(총 분산)을 기반으로 요인을 추출함	변수들 간의 공통 반량(공통 분산)만을 기반으로 하여 요인을 추출함
전체 변수를 가장 잘 설명해 주는 순으로 주성분의 우위가 결정된다	주성분들은 서로 간에 무엇이 더 중요한 변수라는 우위 개념이 없다

• 요인분석을 하기 전에 독립변수들 간의 상관성이 요인분석에 적합한지 검증을 해야 한다
  • 바틀렛 테스트
    • 행력식을 이용하여 카이제곱값을 구하여 각 변수들 사이의 상관계수의 적합성을 검증하는 방법으로 유의확률 p 값으로 나타낸다
      • p 값이 0.05보다 작으면 대각행력이 아니라는(변수들 간에 상관관계가 있다는) 뜻 → 분석에 적합하다고 판단
  • Kaiser-Meyer-Olkin(KMO) 검정
    • 변수들 간의 상관관계가 다른 변수에 의해 잘 설명되는 정도를 나타내는 값을 통계적으로 산출하는 검정 방법
    • 독립변수들 간의 상관계수 제곱들과 편상관계수들을 모두 더한 값에서 상관계수 제곱의 합이 차지하는 비율 값이 KMO 값이다
      • 0.8 이상 → 우수
      • 0.5 이상 → 적합
      • 0.5 미만 → 부적합
  • 검증한 후에는 요인 분석을 통해 생성되는 주성분 변수들의 고슈치를 확인하여 요인의 개수를 결정한다.
    • 고유치: 요인이 설명해 주는 분산의 양 → 요인에 해당하는 변수들의 요인 적재 값의 제곱 합 값들을 합하여 구할 수 있다.
      • 1이면 여인이 변수 하나만큼의 분산을 가지고 있다 → 사회과학에서 고유치가 1 이상인 요인만 선택
        • 총 분산의 60% 이상을 설명해 주는 요인까지 선정하는 것이 일반적이다
          • 설명력이 너무 낮으면 정보의 손실이 커지는 문제가 발생
  • 스크리 도표(scree plot)를 참고하여 적정한 요인의 수를 결정한다 - 엘보우 포인트를 이용함
  • 요인 적재 값(factor loading): 선정된 각 요인이 어떤 변수를 설명해 주는 가를 나타내는 것 → 각 변수와 요인 간의 상관관계의 정도를 확인할 수 있다.
    • 요인 적재 값이 $\pm0.3$ 이상이면 변수와 요인에 유의성이 있다고 할 수 있다 → $\pm0.5$ 이상이면 해당 요인에서 중요한 변수로 판단 → 각 요인이 어떤 변수들의 속성을 갖고 있는지 알 수 있다

다중공선성 해결과 섀플리 밸류 분석

다중공선성(multicollinearity)이란?

• 독립변수들 간의 상관관계가 높은 현상
  • 2개 이상의 독립변수가 서로 선형적인 관계를 나타내는것
• 다중공선성 발생 → 독립변수들 간에는 서로 독립이라는 회귀분석의 전제 가정을 위반하게 된다
  • 추정치의 통계적 유의성이 낮아져 모델의 정합성이 맞지 않는 문제가 발생
    • 회귀모델: 첫 번째 독립변수가 종속변수를 예측하고 두 번째 독립 변수가 남은 변량을 예측하는 식으로 구성 → 다중공선성 발생하면 첫 번째 변수가 설명하고 남은 변량을 두 변째 독립변수가 예측하는 데에 문제 생긴다
• 다중공선성을 판별하는 기준:
  1. 회귀 분석 모델을 실행하기 전에 상관분석을 통해 독립 변수 간의 상관성을 확인하여 높은 상관계수를 갖는 독립변수를 찾아내는 방법
     • 절대치가 0.7 이상이면 두 변수 간의 상관성이 높다 → 다중공선성
     • 단점: 변수가 많을 경우 상관성을 파악하기 힘들다
  2. 회귀분석 결과에서 결정계수 $\text{R}^2$ 값은 크지만 회귀계수에 대한 t값이 낮다면 다중공선성을 의심해 볼 수 있다
     • 종속변수에 대한 독립변수들의 설명력은 높지만 각 계수 추정치의 표준오차가 크다는 것은 독립변수 간에 상관성이 크게 의미해서
     • t값은 해당 변수의 시그널의 강도라고 할 수 있다 → 표준오차(노이즈) 대비 시그널을 뜻함 → 값이 클수록 좋다

     • 적절한 t값:

       

  3. 분산팽창계수(VIF: Variance Inflation Factor)
     • 해당 변수가 다른 변수들에 의해 설명될 수 있는 정도 → VIF가 크다는 것은 해당 변수가 다른 변수들과 상관성이 높다 → 회귀 계수에 대한 분산을 증가시키므로 제거를 해주는 것이 좋다
     • $\text{VIF}_k = \frac{1}{1-\text{R}^2_k}$
       • 다른 변수들에 의해 설명되는 수준이 높을수록 VIF는 큰 값을 가지게 된다
     • $\text{R}^2$는 0에서 1 사이에서 정해지는 것 → VIF 값은 1에서 무한대의 범위를 갖는다
     • 5 이상이면 다중공선성을 의심해 봐야 함 → 10 이상일 때 다중공선성이 있다고 판단
     • VIF 값에 루트에 씌운 값은 해당 변수가 다른 변수들과의 상관성이 없는 경우보다 표준오차가 X배 높다는 것을 의미
       • 어떤 변수의 VIF 값은 16이면 다중공선성이 없는 상태보다 표준오차가 4배 높다
       • 표준오차가 높은 변수는 분석 모델의 성능을 저하시키므로 제거하는 것이 좋
• 다중공선성을 해결하기 위한 가장 기본적인 방법:
  1. VIF값이 높은 변수들 중에서 종속변수와의 상관성이 가장 낮은 변수를 제거하고 다시 VIF 값을 확인하는 게 반복하는 것
     • 특정 변수가 제거 대상이 됐다고 해도 분석 모델의 이론이나 가설에 중요한 역할을 할수도 있으므로 가설과 비즈니스적 요소도 함께 고려하여 변수를 제거해야 된다
  2. 표본 관측치를 추가적으로 확보하여 다중공선성을 완화하는 방법
     • 분석 모수가 많아질수록 회귀계수의 분산과 표준오차가 감소하기 때문이다
     • 관측치를 추가로 확보하는 것은 현실적으로 어렵다 → 잘 쓰이지 않는 방법이다
  3. 변수를 가공하여 변수 간의 상관성을 줄이는 방법
     • 해당 값에 로그를 취하거나 표준화 및 정규화 변환을 해주면 다른 변수와의 높았던 상관성이 완화될 수 있다
     • 연속형 변수를 구간화 혹은 명목변수로 변환할 수도 있다
     • 순수한 변수를 가공하는 것 → 정보의 손실이 발생하긴 함 → 다중공선성 때문에 변수가 제거되는 것보다는 나은 선택이 될 수 있다
  4. 주성분 분석을 통한 변수 축약
     • 주성분 변수는 기존 변수의 변동(상관계수)을 가장 잘 설명하는 변수를 찾아낸 것 → 유사한 변수들을 하나의 변수로 합쳐낸 효과가 있다
     • 하지만 주성분분석을 이용하면 변수의 해석이 어려워진다
     • 실무에서는 순수한 요인 변수들이 직관적이고 관리가 쉽다 → 변수를 축하는 것이 함든 경우가 많다
  5. 데이터 분석 환경에서 제공하는 변수 선택 알고리즘을 활용하는 방법
     • 전진 선택법(forward selection), 후진 제거법(backward elimination), 단계적 선택법(stepwise method) 중 하나를 선택하여 특정 로직에 의해 모형에 적합한 변수를 자동으로 선정

섀플리 밸류(Shapley Value) 분석

• 각 독립변수가 종속변수의 설명력에 기여하는 순수한 수치를 계산하는 방법
• ‘안정적 결혼 문제(Stable Marriage Problem)’ 알고리즘으로 유명한 로이드 섀플리가 개발한 독립변수의 설명력 분배 방법이다
• 해당 변수를 모델에 투입했을 때 설명력에 어느 정도의 기여를 하는지 측정힐 수 있는 기준값으로 활용할 수 있다.

데이터 마사지와 블라인드 분석

데이터 마사지

• 데이터 분석 결과가 예상하거나 의도한 방향과 다를 때 데이터의 배열을 수정하거나 관점을 바꾸는 등 동일한 데이터라도 해석이 달라질 수 있도록 유도하는 것
• 데이터 마사지도 결국 분석가의 주관적 판단이 개입되는 것이라 지양해야 한다

  데이터 마사지 방법

  1. 편향된 데이터 전처리
  • 이상치나 결측값 등의 전처리를 분석가가 의도하는 방향에 유리하도록 하는 것
    1. 매직 그래프 사용
  • 그래프의 레이블 간격이나 비율을 왜곡하여 수치의 차이를 실제보다 크거나 작게 인식하도록 유도하는 방법
  • 데이터 조작과 다름없는 방법이라서 절대 사용해서는 안되며 매직그래프에 속지 않도록 주의해야 된다
    1. 분모 바꾸기 등 관점 변환
  • 동일한 비율 차이라 하더라도 분모를 어떻게 설정하는가에 따라 받아들여지는 느낌이 달라질 수 있다
    1. 의도적인 데이터 누락 및 가공
  • 데이터 분석가가 원하는 방향과 반대되는 데이터를 의도적으로 누락시키거나 다른 수치와 결합하여 특성을 완화시키는 방법
    1. 머신러닝 모델의 파라미터 값 변경 및 연산반복
  • 모델의 파라미터 값을 변경해 가며 다양하게 연산을 반복하다 보면 머신러닝 모델의 결과가 원하는 대로 조정될 수 있다
    1. 심슨의 역설
  • 데이터의 세부 비중에 따라 전체 대표 확률이 왜곡되는 현상을 의도적으로 적용하여 통계 수치를 실제와는 정 반대로 표현할 수 있다 → 데이터 왜곡에 당하거나 직접 하지 않게 위해 잘 이해하고 있어야 한다

블라인드 분석

• 데이터 마사지에 의한 왜곡을 방지하는 방법
• 인지적 편향(혹은 확증 편향)에 의한 오류를 최소화하기 위한 방법
  • 편향을 완벽히 방지할 수 있는 것도 아님 → 기존 방법보다 오히려 의미 없는 결과를 도출하게 될 수도 있다
• 분석의 목적이 분석가의 부정행휘를 막기 위한 것은 아님 → 사용 목적을 잘 이해하고 수행을 해야 한다
• 기존에 분석가가 중요하다고 생각했던 변수가 큰 의미가 없는 것으로 결과가 나왔을 때 무리해서 의미부여를 하거나 그 변수에 집착하여 해석에 유리하도록 변수를 가공하게 되는 실수를 방지라는 목적이 크다

Z-test와 T-test

• 집단 내 혹은 집단 간의 평균값 차이가 통계적으로 유의미한 것인지 알아내는 방법
• 단일 표존 집단의 평균 변화를 분석하거나 두 집단의 평균값 혹은 비율 차이를 분석할 때 사용
• 분석하고자 하는 변수가 충족되어야 하는 조건:
  1. 양적 변수이다
  2. 정규 분포이다
  3. 등분산
• 두 분석 방법을 선택하는 기준은 모집단의 분산을 알 수 있는지의 여부와 표분의 크기에 따라 달라진다

Z-test	T-test
본래 모집단의 분산을 알 수 있는 경우에 사용된다 (BUT 모집단의 분산을 알 수 있는 경우 거의 없다)	표본의 크기가 30미만이어서 표본 집단의 정규분포를 가정할 수 없을 때 사용된다
표본의 크기가 30이상이면 정규분포를 따른다고 볼 수 있으므로 Z-test 사용이 가능	표본의 집단의 크기가 30이상일 때도 사용 가능이라서 일반적으로 T-test를 사용한다.

T-test

• 계산 방식:
  • \[t_{stat} = \frac{\overline{X}-\mu}{\frac{S_X}{\sqrt{n}}}\]
    • $\overline{X}$: 표본 평균
    • $\mu$: 귀무 가설에서의 모평균
    • $S_X$ 집단 값 차이의 표준편차
    • $n$: 표본 크기
• 두 집단의 T-test를 하는 공식:
  • \[t_{stat} = \frac{\overline{X}_A - \overline{X}_B - (\mu_A - \mu_B)}{\sqrt{\frac{S^2_A}{n_A}+\frac{S^2_B}{n_B}}}\]
• 단일 집단의 비율 차이 검정 공식:
  • \[t_{stat} = \frac{p-\pi}{\sqrt{\frac{\pi(1-\pi)}{n}}}\]
    • $p$: 변화된 후의 비율
    • $\pi$: 변화 전의 비율 혹은 귀무가설의 추정 비율
• 두 집단의 비율 차이 검정 공식
  • \[t_{stat}=\frac{(p_A-p_B)-(\pi_A-\pi_B)}{\sqrt{\frac{p_A(1-p_A)}{n_A}+\frac{p_B(1-p_B)}{n_B}}}\]

Z-test

• 계산 방식:
  • \[Z_{stat} = \frac{\overline{X} - \mu}{\frac{\sigma_X}{\sqrt{n}}}\]
    • $\sigma_X$: 모집단의 표준편차

Analysis of Variance(ANOVA)

• 세 집단 이상의 평균을 검정할 때는 사용한다
• 연속확률분포인 F분포를 사용한다
  • F검정의 통곗값은 집단 간 분산의 비율을 나타낸다 → 분산 분석이라 불림
  • 두 모분산의 비교 및 검정을 위해 사용
• ANOVA나 회귀분석에서 F분포를 통해 독립변수가 종속변수에 미치는 영향을 분석 → ANOVA는 집단의 종류(독립변수)가 평균 값의 차이 여부(종속변수)에 미치는 영향을 검정하는 것
  • 회귀분석도 그렇기 때문에 회귀분석과 비슷한 면이 있다
• 가설:
  • $H_0$(귀무가설): 독립변수(인자)의 차이에 따른 종속변수(특성 값)는 동일한다
  • $H_1$(대립가설): 독립변수(인자)의 차이에 따른 종속변수(특성 값)는 다르다
• 독립변수인 요인의 수에 따라서 다르게 부름
  • 더 많은 N 가지라면 N원 분산분석(N-way ANOVA)이라고 함
• 독립변수는 집단을 나타낼 수 있는 범주(분류)형 변수이어야 하며, 종속변수는 연속형 변수이어야 한다
• 각 집단의 평균값 차이가 통계적으로 유의한지 검증 → 각 집단의 평균이 서로 멀리 떨어져 있어 집단 평균의 분산이 큰 정도를 따져서 집단 각 평균이 다른지를 판별한다
  • 이러한 요소로 집단 내의 각 관측치들이 집단 편균으로부터 얼마나 퍼져 있는지를 나타내는 집단 내 분산이 사용되며, 전체 집단의 통합 평균과 각 집단의 평균값이 얼마나 퍼져 있는지를 나타내는 집단 각 평균의 분산이 사용된다
• 집단 간 평균의 분산을 집단 내 분산으로 나눈 값이 유의도 임계치를 초과하는가에 따라 집단 간 평균 차이를 검정
• ANOVA의 공식:
  • \[\frac{\frac{\sum_j\sum_i(\overline{y}_j - \overline{y})^2}{k-1}}{\frac{\sum_j\sum_i(y_ij - \overline{y}_j)^2}{n-k}} = \frac{\frac{SS_b}{k-1}}{\frac{SS_w}{n-k}} = \frac{MS_b}{MS_w}=F\]

  • 공식을 좀 더 이해하기 편하도록 ANOVA 공식 표로 표현할 수 있다.

    

카이제곱 검정(교차분석)

• 명목 혹은 서열척도와 같은 번주형 변수들 간의 연관성을 분석하기 위해 결합분포를 활용하는 방법
• ‘연령’과 같은 비율척도 변수는 ‘연령대’와 같은 서열척도로 변환해서 사용해야 한다
• 기본 원리: 변수글 간의 범주를 동시에 교차하는 교차표를 만들어 각각의 빈도와 비율을 통해 변수 상호 간의 독립성과 관련성을 분석하는 것이다
• $\chi^2_{ij}$ 계산 방법:
  • \[\frac{\text{실제빈도}_{ij}-\text{기대빈도}_{ij}}{\text{기대빈도}_{ij}}\]

머신러닝 분석 방법론

선형 회귀분석과 Elastic Net(예측모델)

회귀분석의 기원과 원리

• $\text{X, Y}$ 좌표에 산점도를 찍고 $\text{X와 Y}$의 관계를 가장 잘 나타낼 수 있는 직선을 찾는 것이다
• 해당 객체가 소속된 집단의 X(독립변수) 평균값을 통해 Y(종속변수) 값을 예측하는 것이다 → 종속변수 Y의 값에 영향을 주는 독립변수 X들의 조건을 고려하여 구한 평균값
  • 절펴느 기울기, 오차항으로 이루어짐 → 회;분석은 오차항을 최소화하는 절편과 기울기를 구하는 것
    • 오차항: 독립변수가 종속변수에 주는 영향력을 제외한 변화량
    • \[y = \beta_0 + \beta_1X_1+ ... +\beta_nX_n + \epsilon\]
      • $\beta_0$: 절편
      • $\beta_1$~$\beta_n$: 가중치
      • $\epsilon$: 전차

        최적 모델 구하는 방법

• 모형 적합이라 부름 → 회귀선과 각 관측치를 뜻하는 점 간의 거리를 최소화하는 것
• 예측치와 관측치들 간의 수직 거리(오차)의 제곱합을 최소로 하는 직선이 회귀선 → 최소제곱추정법(least squares elimination)
  • 최대우도추정법(maximum likelihood estimation)과 동일한다 → 독립변수가 주어졌을 때 예측값이 관측된 가능도를 최대화하는 것

회귀분석

• 단순 회귀분석 (혹은 단변량 회귀분석) → 독립변수가 하나인 회귀분석
• 다중 회귀분석 → 독립변수가 두개 이상인 회귀분석
• 독립변수 간에 상관관계가 없어야 한다 → 다중 회귀분석 할 때는 다중공선성을 검사를 해야 한다
• 충족되어야 하는 기본 조건
  1. 잔차의 정규성: X에 해당되는 Y의 값들의 전차는 정규분포를 해야 한다
  2. 잔차의 등분산성: 잔차의 분산은 회귀 모형의 독립 변숫값과 상관없이 일정해야 한다
  3. 선형성: X 값의 변화에 따른 Y 값의 변화는 일정해야 한다

다항 회귀(Polynomial Regression)

• 독립변수와 종속변수의 관계가 비선형 관계일 때 변수에 각 특성의 제곱을 추가하여 회귀선을 비선형으로 변환하는 모델
• 차수가 커질수록 편향은 감소하지만 변동성이 증가하게 된다 → 분산이 늘어나고 과적합을 유발할 수 있다

변수 선택 알고리즘

1. 전진 선택법: 절편만 있는 모델에서 시작하여 유의미한 독립변수 순으로 변수를 차례로 하나씩 추가하는 방법
   • 빨라서 좋긴 하지만 한 번 선택된 변수를 다시 제거되지 않는다
2. 후진 제거법: 모든 독립변수가 포함된 상태에서 시작하여 유의미하지 않는 순으로 설명변수를 하나씩 제거하는 방법
   • 시간 오래 걸릴 수 있긴 하지만 유의미한 변수를 처음부터 모두 넣고 시작해서 전진선택법보다 더 안전한 방법다다
3. 단계적 선택법: 변수 하나씩 추가하기 시작하면서, 선택된 변수가 3개 이상이 되면 변수 추가와 제거를 번갈아 가며 수행
   • 단순히 종속변수와의 상관도가 높은 독립변수를 선택하는 것에서 더 나아가, 선택된 독립변수 모델의 잔차를 구하여 선택되지 않은 나머지 변수와 잔차의 상관고를 구하여 변수를 선택한다.
4. Least Angle Regression(LARS)
5. Genetic Algorithm
6. Elastic Net

Ridge와 Lasso 그리고 Elastic Net

Ridge

• 전체 변수를 모두 유지하면서 각 변수의 계수 크기를 조정
  • 종속변수 예측에 영향을 거의 미치는 않는 변수는 0에 가까운 가중치를 주게 하여 독립변수들의 영향력을 조정해 주는 것 → 조정을 계수는 정규화라고 함
• aka L2-norm → 매개변수 $\alpha$의 값을 조정하여 정규화 수준을 조정해 준다
  • $\alpha$값이 0이면 선형회귀와 동일해지고, 값이 클수록 독립변수들의 영향력이 작아져 회귀선이 평균을 지나는 수평선 형태가 된다.

Lasso

• 중요한 몇 개의 변수만 서택하고 나머지 변수들은 계수를 0으로 주어 변수의 영향력을 아예 없앤다
• aka L1-norm → Ridge처럼 $\alpha$값을 통해 정규화의 강도를 조정

Elastic Net

• Ridge와 Lasso의 최적화 지점이 다르기 때문에 두 정규화 항을 결합하여 절충한 모델이다
  • Ridge는 변환된 계수가 0이 될 수 없지만 Lasso는 0이 될수 있다는 특성을 결합하는 것
• Ridge와 Lasso의 혼합비율(r)을 조절하여 모델의 성능을 최적으로 끌어낼 수 있다
  • 0에 가까울수록 Ridge와 같아진다
  • 1에 가까울수록 Lasso와 같아진다
  • 독립변수를 이미 잘 정제해서 중요한 것으로 판단되는 변수들만 선별해서 모델에 넣은 상태면 Ridge의 비율을 높이는 것이 좋고 변수 선택 없이 주어진 독립변수를 모두 집어넣은 상태라면 Lasso의 비율을 높이는 것이 좋다

로지스틱 회귀 분석 (분류 모델)

• 어떤 카테고리에 들어갈지 분류를 하는 모델
• 이항(binary)으로 이루어져 두 카테고리 중에 어느 카테고리에 들어가는지 예측
  • 종속변수의 범주가 3개 이상 → 다항 로지스틱 회귀분석
• 선형회귀식의 사상은 그대로 유지하되 종속변수를 1이 될 확률로 변환하여 그 확률에 따라 0과 1의 여부를 예측
• Odds: 사건이 발생할 가능성이 발생하지 않을 가능성보다 어느 정도 큰지를 나타내는 값
  • 로짓 회귀선으로 변환해주기 위해
  • \[Odds = \frac{P(\text{event occurring})}{P(\text{event not occurring})}\]
  • 오즈 값에 로그를 취하면 양의 무한대에서 음의 무한대를 갖는 형태가 된다 → 0에서 1사이의 범위를 나타내지 못하는 문제 → Sigmoid 함수
    • 확률을 로짓 변환하여 0에서 1사이 치환해 주는 함수

의사결정나무와 랜덤포레스트

분류나무와 회귀나무

• 의사결정나무는 명목형의 종속변수를 분류할 수 있는 분류나무와 연속형의 수를 예측할 수 있는 화귀나무가 있다

분류나무

• 각 노드들은 포함된 관측치들의 비육과 개수를 표시해주며 포함된 카테고리의 비율에 따라 노드의 카테고리가 결정된다
• 분류나무를 해석할 때는 더 이상 나눠지지 않는 끝에 있는 노드들을 기준으로 분류 조건과 군집을 봐야 한다
• 카테고리를 가장 잘 나눠줄 수 있는 기준을 찾아내는 방법:
  • 불순도를 낮추기 → 정보 획득량
    • 지니 계수
    • 엔트로피
  • 순도를 높이기

회귀나무

• 지니 계수나 엔트로피 대신 잔차 제곱합 등의 분류 기준을 사용
• 종속변수의 비선형에 영향을 받지 않는다 → 선형회귀분석에 비해 모델 활용이 까다롭지 않다
• 끝 노드에 속한 데이터 값의 평균을 구해 회귀 예측값을 계산
• F-value나 분산의 감소량을 분류 기준으로 사용
  • 크다는 것은 노드 간의 이질성이 높다는 것을 의미
  • 최대한 커ㅓ니는 방향으로 자식 노드를 나눈다

의사결정나무 모델의 장간점

• 직관적이고 어렵지 않기 떄문에 해석의 용이성 측면에서 높은 높은 평가를 받는다
• 비선형 모델이기 때문에 회귀분석과 같이 데이터의 선형성, 정규성, 등분선성 등이 필요하지 않다
• 일반 회귀 보델의 경우 명목형 변수는 예측 데이터에 있는 정보가 학습 데이터에 없으면 예측이 불가능하다
• 과적합괼 확률이 높다

의사결정나무 모델 과적합 방지 위한 방법

• 가지치기와 정보 획득량 임곗값 설정, 한 노드에 들어가는 최소 데이터 수 제한하기, 노드의 최대 깊이 제한하기
• Pruning: 모델의 분기 가지들을 적절히 쳐내어 과도하게 세밀하게 분기된 부분들을 없애 주는 것
• 분기를 했을 때 정보 확득량이 너무 적으면 분기를 멈추도록 설정하는 것

랜덤 포레스트

• 나무 여러개 만들어서 학습을 하는 것
• • 다양한 상황을 고려하여 학습이 되기 때문에 과적합 방지 할 수 있다
• 여러 모델의 결과를 종합적으로 봐서 합리적인 선택을 하는 집잔지성과 같은 개념 → 앙상블 학습
• Bootstrap: 데이터셋 중복을 허용하여 무작위로 여러 번 추출하는 것
• Bagging: bootstrap aggregating의 약자로 여러 개의 의사결정 나무를 하나의 모델로 결합해주는 것
  • 분류 모델의 경우 투표 방식으로 집계하며 연속형 값의 예측 모델인 경우 평균으로 집계한다
    • 유사한 개념으로 부스팅 → 맞추기 어려운 문제를 맞히는 게 거 특화된 방식