데이터 분석2-1: 데이터 전처리와 파생변수 생성

결측값 처리

• 실제 분석 프로젝트에서 다루는 대부분의 데이터는 결측값이나 이상치가 많기 때문에 데이터 탐색 단계에서 파악한 문제점들을 처리하는 과정이 필요한다.
• 결측값:
  • 분석 환경에 따라 ‘.’, ‘NA’, ‘NaN’ 등으로 표시된다
  • 3가지 종류:
    • 완전 무작위 결측 (MCAR: Missing Completely at Random)
      • 결측값이 무작위로 발생한 경우
    • 무작위 결측 (MAR: Missing at Random)
      • 다른 변수의 특성에 의해 해당 변수의 결측치가체계적으로 발생한 경우
    • 비무작위 결측 (MNAR: Missing Not at Random)
      • 결측값들이 해당 변수 자체의 특성을 갖고 있는 경우
• 가장 간단한 방법 (전체 데이터에서 결측값 비율이 10% 미만일 경우 사용함)
  • 심하게 많은 변수를 제거한다.
  • 표본 제거 방법(Complete case analysis): 결측값이 포함된 행을 제외하고 분석
• 두 방법은 결측값 비율은 높은 경우에 적용하면 데이터가 편중되어 편행이 발생한 위험도 있어서 다른 처리 방법을 적용해야 된다.

평균 대치법 (Mean Imputation)이란?

• 결측값을 제외한 온전한 값들의 평균을 계산하고 결측값들에 대치하는 것이다.
• 위 두 방법 외에 대표적인 결측치 처리 방법이다.
  • 유사한 방법으로 최빈값, 중앙값, 최댓값, 최솟값 대치도 있다.
• 표본제거방법처럼 완전 무작위 결측이 아닌 경우 적절하지 않은 방법인다.

보간법 (Interpolation)

• 전, 다음 시점의 값 기준 대치하는 기법이다
  • 전 시점 혹은 다음 시점의 값으로 대치하는 것
  • 전 시점과 다음 시점의 평균 값으로 대치하는 것
• 데이터가 시계열적 특성을 가지고 있는 경우 효과적인 방법이다.

회귀 대치법 (Regression Imputation)

• 해당 변수와 다른 변수 사이의 관계성을 고려하여 결측값을 계산하는 것
• 추정하고자 하는 결측값을 가진 변수를 종속변수로 하고, 나머지 변수를 독립 변수로 하여 추정한 회귀식을 통해 결측값을 대치하는 것이다.
• 독립 변수의 조건부 평균으로 결측값을 대치하는 것에 결측된 변수의 분산을 과소 추정하는 문제를 생길 수 있다.
  • 해결법: 확률적 회귀대치법(Stochastic Regression Imputation) → 변동성을 조정할 수 있다.
    • 인위적으로 회귀식에 확률 오파항을 추가하는 기법이다.
    • 즉, 관측된 값들을 변동성만큼 결측값에도 같은 변동성을 추가해 주는 것이다.
      • 어느 정도 표본오차를 과소 추정하는 문제를 가지고 있다.

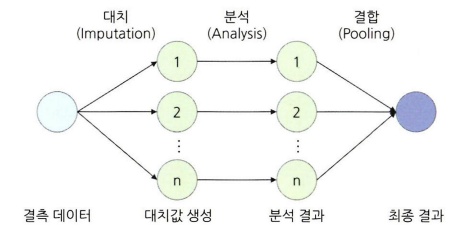
다중 대치법 (Multiple Imputation)

• 표본오차를 과소 추정 문제를 해결하기 위한 요즘 많이 사용되는 기법이다.
• 단순대치를 여러 번 수행하여 n 개의 가상적 데이터를 생성하여 이들의 평균으로 결측값을 대치하는 방법 → 3가지 단계
  • 대치 단계
    • 가능한 대치 값이 분포에서 추출된 서로 다른 갑스로 결측치를 처리한 n개의 데이터셋 생성
    • 몬테카를로(MCMC: Markov Chain Monte Carlo) 방법이나 연쇄식을 통한 다중 대치(MICE: Multivariate Imputation by Chained Equation)를 사용하여 대치값을 임의로 생성한다.
      • 결측값의 비율이 증가할수록 가상데이터도 많이 생성해야 검정력이 증가한다.
  • 분석 단계
    • 생성된 각각의 데이터셋을 분석하여 모수의 추정치와 표준오차 계산
  • 결합 단계
    • 계산된 각 데이터셋의 추정치와 표준오차를 결합하여 최종 결측 대치값 산출

이상치 처리

• 이상치: 일부 관측치의 값이 전체 데이터의 범위에서 크게 벗어난 아주 작거나 큰 극단적인 값을 갖는 것이다.
  • 데이터의 모집다 평균이나 총합을 추정하는 것에 문제를 일으키며 분산을 과도하게 증가시켜 분석이나 모델링의 정확도를 감소시킨다 → 제거하면 좋다
    • 전체 데이터의 양이 많을수록 이상치 영향력이 줄어든다 → 제거의 필요성이 낮아진다
• 처리 방법:
  1. 해당 값을 결측값으로 대체한 다음 결측값 처리를 하는 것
  2. trimming: 아예 해당 이상치를 제거하는 것
     • 둘다 간단하긴 하지만 추정치의 분산은 감소하지만 실젯값을 과장하여 편향을 발생시킨다 → 관측값 변경 (value modification)
     • 하한 값과 상한 값을 결정한 후 하한 값 보다 작으면 하한 값으로 대체하고 상한 값보다 크면 상한 값으로 대체하는 기법 → 가중치 조정 (weight modification)
     • 이상치의 영향을 감소시키는 가중치를 주는 기법
• EDA나 시각화 기법을 사용하여 이상치를 확인할 수 있다.
  • 이상치를 선정하는 가장 일반적인 방법:
    1. 박스플롯 상에서 분류된 극단치를 그대로 선정하는 방법
    2. 임의로 허용범위를 설정하여 이를 벗어나는 자료를 이상치로 정의하는 방법
       • 평균은 이상치에 통계량이 민감함 → 이상치에 보다 강건한 중위수와 절대 편차(MAD: Median Absolute Deviation)를 사용하는 것이 더 효과적이다.
• 해당 데이터 변수들의 의미와 비즈니즈 도메인을 먼저 이해하고 이상치가 생긴 원인을 논리적으로 생각하여 데이터를 바라봐야 효과적인 이상치 탐색을 수행할 수 있다.
• 분석 도메인에 따라 이상치가 중요한 분석 요일일 수 있다 → 특히 제조 공정 데이터 분석의 경우

변수 구간화(Binning)

• 이산형 변수를 범위형 변수로 변환하는 것
  • 데이터 분석의 성능을 향상시키기 위해
  • 해석의 편리성을 위해
  • 예시: 나이 변수를 10대, 20대, 30대대와 같이 특정 간격으로 나눔
• 각 범주에 해당되는 관측치의 수가 유사해지도록 하여 범주별 분포가 일정하도록 구간화를 하는 방법도 사용한다.
  • 이산형 변수를 범주형 변수로 비즈니스적 상황에 맞도록 변환시킴으로써 데이터의 해석이나 예측, 분류 모델을 의도에 맞도록 유도할 수 있다.
• 다른 방법:
  1. 이산 값을 평활화(smoothing)하여 단순한 이산 값으로 변환시키는 기법
     • 변수의 값을 일정한 폭(width)이나 빈도(frequency)로 구간을 나눈 후, 각 구간 안에 속한 데이터 값을 평균, 중앙값, 경곗값 등으로 변환해 주는 것
  2. 머신러닝 기법
     • 클러스터링
       • 타깃 변수 설정이 필요 없이 구간화할 변수의 값들을 유사한 수준끼리 묶어줄 수 있는 것
     • 의사결정나무
       • 타깃 변수를 설정하여 구간화할 변수의 값을 타깃 변수 예측에 가장 적합한 구간으로 나누어 주는 것
• 변수값이 효과적으로 구간화댔는지 측정할 수 있는 방법:
  • Weight of Evidence (WOE) 값
  • Information Value (IV) 값
    • IV 수치가 높을수록 종속변수의 True와 False를 잘 구분할 수 있는 정보량이 많다는 뜻 → 변수가 종속변수를 제대로 설명할 수 있도록 구간화가 잘되면 IV값이 높아지는 것
    • IV값에 따른 해석 방법

IV값 기주	해석
0~0.2	의미 없음
0.02~0.1	약한 예측
0.1~0.3	중간 예측
0.3~0.5	강한 예측
0.5~1	과도한 예측(확인 필요)

데이터 표준화와 정규화 스케일링

• 독립 변수들이 서로 단위가 다르거나 편차가 심할 때 값의 스케일링을 일정한 수준으로 변환시켜주는 기법
• 독립 변수 간 단위가 다른 것은 회귀분석이나 의사결정나무 등 대부분의 데이터 마이닝 모델의 분석 결과에 별다른 영향을 미치지 않는다 → 그대로 사용해도 무방하긴 함 → 표준화나 정규화는 특정 머신러닝 모델의 학습 효율을 증가시킨다 → 많이 사용함
  • 해석적 관점에서 유용하다

    표준화

• 각 관측치의 값이 전체 평균을 기준으로 어느 정도 떨어져 있는지 나타낼 때 사용함
• 평균은 0으로 변환되고 1표준편차 거리는 $\pm{1}$, 2표준편차 거리는 $\pm{2}$로 변환된다.
  • Zero-mean으로부터 얼마나 떨어져 있는지를 나타낸다 → Z-score라 표현함 \(z = \frac{x - \mu}{\sigma}\)

    정규화

• 데이터의 범위를 0부터 1까지로 변환하여 데이터 분포를 조정하는 방법
• 전체 데이터 중에서 해당 값이 어떤 위치에 있는지 파악하는 데에 유용하다
  • 0에 가까워지면 작은 값이다
  • 1에 가까워지면 큰 값이다 \(x_{scaled} = \frac{x - x_{min}}{x_{max} - x_{min}}\)

표준화	정규화
특정 값이 평균에서 얼마나 떨어져 있는지 나타냄	특정 값이 평균으로부터 어느 정도 떨어져 있는지를 바로 알기 함들다
가장 큰 값이 무조건 1이 되는 것 아니다 (다른 값도 될 수 있다)	가장 큰 값은 1이고 가장 작은 값은 0이다

• 기본 표준화, 정규화 방식은 이상치에 만감하다는 단점을 가진다 → RobustScaler
  • 데이터의 중앙값(Q2)을 0으로 잡고 Q1(25%)과 Q3(75%) 사분위수와의 IQR 차이를 1이 되도록 하는 스케일링 기법
  • 이상치의 영향력을 최소화하여 일반적으로 표준화, 정규화보다 성능이 우수한 것으로 알려져 있다.
• K-NN, SVM과 같은 거리를 활용한 군집 분석에서 필수적이다
  • 관측치가 군집의 중심점 혹은 다른 관측치와 어누 정도로 거리가 떨어져 있는지 측정함으로써 군집을 나눔 → 변수(차원)마다 스케일링이 제각각 이면 군집이 제대로 분리될 수 없어서

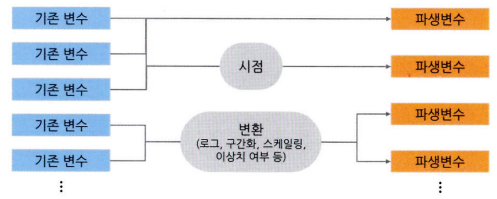
모델 성능 향상을 위한 파생 변수 생성

• 파생 변수(Derived variable)란?
  • 원래 있던 변수들을 조합하거나 함수를 적용하여 새로 만들어낸 변수
    • ex:
      • $x_1$, $x_2$ 두 변수의 평균값으로 만드 $x_3$
      • 데이터 구간화, 표준화 및 정규화 등도 일종의 파생변수라 할 수 있다
      • 기존 값에 로그나 제곱근 등을 취해 변동성을 환화시키는 것
      • 지수함수를 사용하여 분산능 증폭시키는 것
      • 시점을 고려하여 과거 시점 대비 변화 정도를 파생변수로 만드는 것
• 데이터의 특성을 이용하여 분석 효율을 높이는 것 → 전체 데이터에 대한 파악이 중요하다
  • 또한 해당 비즈니스 도메인에 대한 충분한 이해가 있어야 한다
• 기존의 변수를 활용해서 만들어낸 변수 → 다중공선성 문제가 발생할 가능성이 높다 → 파생변수를 만든 다음에는 상관분석을 통해 변수 간의 상관성을 확인해야 한다.
  • 상관성에 따라 파생변수를 그대로 사용할지, 기존 변수를 제외하고 파생변수만 사용할지 여부를 결정
  • 변수들 조합의 주요 속성만 추출해내는 주성분 분석(PCA) 등을 사용할 수 있다.

슬라이딩 윈도우 데이터 가공

• 슬리이딩 윈도우란?
  • 본래 실시간 네트워크 패킷 데이터를 처리하는 기법
• 현재 시점으로부터 $\pm{M}$ 기간의 데이터를 일정 간격의 시간마다 방식이다
  • 특징: 각각의 데이터 조각(window)들이 서로 겹치며 데이터가 전송되는 것
• 데이터를 겹쳐 나눔으로써 전체 데이터가 증가하는 원리를 차용한 것이 슬라이딩 윈도우 데이터 가공의 핵심이다
• 단점:
  • 데이터가 충분하지 않을 경우 예측력이 좋은 모델을 만드는 것이 쉽지는 않다.
  • 학습 데이터의 시기와 예측 데이터의 시기와의 시점 차이가 크면 예측력이 떨어질 위험이 크다
    • 현재 상황을 반영하지 않은 데이터로 학습해서
    • 슬라이딩 윈도우 방법을 확용하면 많은 분석 데이터셋을 확보하고 학습데이터의 최근성을 가질 수 있다.

범주형 변수의 가변수 처리

• 가변수(Dummy variable) 처리란?
  • 범주형 변수를 0과 1의 값을 가지는 변수로 변환해 주는 것 → 이진변수, 불리언 변수라고도 함
  • 예시:
    • 남성은 0, 여성은 1인 식으로 변환한다.
    • 흡연 여부 0, 1로 변환한다
• 범주형 변수는 사용할 수 없고 연속현 변수만 사용 가능한 분석기법을 사용하기 위해
• 범주가 3개 이상인 경우? → $(\text{범주 개수} - 1)$ 개 가변수를 OHE처럼 생성 → 모두 생성된 가변수가 0일 경우 당연히 마지막 범주가 1인 것임을 알 수 있어서 장황
  • 제거된 범주를 baseline이라고 함
    • 해당 없음도 필요한 경우 → 해당 없음은 하나의 범주이라 baseline이 된다
    • baseline 범주를 기반으로 각각 범주들의 종속변수에 대한 영향력을 산출한다 → baseline 범주의 종속변수에 대한 영향력은 0으로 맞춰짐 → baseline 범주 대비 다른 범주들의 영향력이 산출되는 것이다
• 각각의 가변수는 독립성을 가지고 있어야 한다 → 독립변수 간에는 서로 영향을 주지 않아야 한다
  • 독립변수 간에 강한 상관성이 존재 → 다중공선성(multicollinearity) 문제 발생 → 하나의 범주의 가변수를 제거하게 되어야 변수 간의 독립성을 얻을 수 있다.

클래스 불균형 문제 해결을 위한 언더샘플링과 오버샘플링

• 클래스 불균형(Class disparity)이란?
  • 한 타깃 값의 비율 매우 적은(혹은 많은) 경우
  • 심하게 되면 원하는 대로 학습이 제대로 이루어지지 않아 예측 정확도가 떨어지게 된다 → 데이터가 다양성을 가지고 있어야 모델을 잘 학습시킬 수 있다.
• 일반적인 기계학습 분류 모델은, 적은 비중의 클래스 든 큰 비중의 클래스 든 중요도에 차별을 두지 않고 전체적으로 분류를 잘 하도록 학습된다 → 데이터는 90:10 클래스 비율을 가지면 10의 비중을 가진 클래스가 분류가 잘 안 되더라도 전체적인 분류 정확도가 높은 방향으로 학습된다.
• 해결 방법:
  1. 가중치 밸런싱 (Weight balancing)
     • 모델 자체에 중요도가 높은 클래스에 정확도 가중치를 주어, 특정 클래스의 분류 정확도가 높아지도록 조정해 주는 것 → 분류 모델은 전체 정확도를 높이는 방향으로 학습된다고 함 → 잘못 분류한 비중을 최소화하도록 학습하는 것
       • 분류 예측에 따른 손실(Loss)이라 한다
         • 손실을 계산하여 손실이 최소화되도록 학습함 → 가중치 밸련싱은 중요도가 높은 클래스를 잘못 분류하면 더 큰 손실을 계산하도록 조정함
  2. 불균형 데이터 자체를 균형이 맞도록 가공한 다음 모델을 학습하는 것
     • 큰 비중의 클래스의 데이터를 줄이기 → 언더샘플링(undersampling)
       • 큰 비중의 클래스 데이터를 작은 비중의 클래스 데이터만큼만 추출하여 학습시키는 것
       • 기법:
         1. 랜덤 언더샘플링(Random undersampling)
            • 작은 비중의 클래스와 관측치 비육이 유사해질 때까지 무작위로 큰 비중의 클래스의 관측치를 제거하는 단순한 방식이다다
         2. EasyEnsemble
            • 일종의 앙상블 기법 → 큰 비중의 클래스를, N개의 작은 비중의 클래스와 동일한 크기의 데이터셋으로 분리함
            • 일반적으로는 분류 가중치의 평균을 구하여 최종 분류 값을 산출한다.
         3. Condensed Nearest Neighbour
            • K-근점이웃 모델을 차용한 언더샘플링 방법 → 비중이 큰 클래스의 관측치 중에서 비중이 작은 클래스와 속성값이 확연히 다른 관측치들은 제거하여 굳이 학습에 사용하지 않아도 되는 관측치를 제거하는 것
              • 비중이 큰 클래스의 관측치 중 비중이 적은 클래스와 공간상 위치가 맞닿는 부분의 관측치만 남기는 것
            • 기법:
              1. 비중이 작은 클래스만 있는 집합 S에, 비중이 큰 클래스의 관측치 하나를 포함시킨다
              2. 포함시킨 비중이 큰 클래스의 관측치를 K-NN 방식으로 분휴한다 → 기본적으로는 1NN
              3. 만약 분류가 틀렸으면 그 표본을 집합 S에 포함시킨다
              4. 집합 S에 포함되어 있는지 않은 모든 값의 분류가 집합 S로 배정이 가능할 때까지 1~3번을 반복한다
     • 작은 비중의 클래스 데이터를 늘리기 → 오버샘플링(oversampling)
       • 작은 비중의 클래스의 관측치 수와 동일하도록 작은 비중의 클래스의 관측치들을 증가시킨다.
       • 기법:
         1. 작은 클래스의 관측치를 단순히 무작위로 선택하여 반복 추출하는 방식
            • 단순히 동일한 관측치가 복제되는 것 → 정보의 양은 증가하지 않음 → 정보의 손실은 없지만 모델의 과적합이 발생할 가능성이 있다 → 간단한 방식이지만 좋은 기법은 아님
         2. Synthetic Minority Oversampling Technique (SMOTE) → 대표적인 오버샘플링 기법
            • CNN 비슷하게 K-NN 기법을 사용함 → 비중이 작은 클래스의 관측치의 K-최근접 이웃 관측치들을 찾아서, 해당 관측치와 K개 이웃 관측치들 사이의 값을 가진 새로운 관측치들을 생성함
         3. Adaptive Synthetic Sampling Approach(ADASYN) → SMOTE 기법을 발전시킨 방식
            • 기존 SMOTE 방식에 오버샘플링할 관측치의 양을 체계적으로 조절할 수 있는 장점을 가진다
            • 새부 알고리즘:
              1. 클래스 불균형의 정도를 측정한다
              2. 작은 비중의 클래스에 속하는 관측치들의 K-NN 중 큰 비중의 클래스에 속하는 관측치의 비율을 구한다 → $r_i$이라 함
              3. 모든 작은 비중의 클래스의 관측치에 대한 $r_i$ 값을 구해, $r_i$ 값을 표준화한다 → $\hat{r_i} = \frac{r_i}{\sum_{i}{r_i}}$
              4. 클래스의 균형을 맞추기 위해 오버샘플링해야 하는 관측치의 수를 $\hat{r_i}$에 곱하여 $g_i$를 구한다 → $g_i = r_i \times \text{resampled N}$
              5. 각 $g_i$에 $x_i$를 대응시키고, $x_i$에 대응되는 K-NN 중 작은 비중의 클래스에 속하는 관측치에서 임의의 하나를 뽑는다
              6. 5번에서 뽑은 관측치와 $x_i$ 사이에 임의의 synthetic sample을 만든다
              7. 5번의 작은 비중의 클래스에 속한 모든 $x_i$에 대해 5번과 6번을 $g_i$만큼 반복한다.
            • ADASYN은 borderline SMOTE와 유사하게 경곗값에 가중치를 주어 샘플을 생성
       • 적용할 때에는 먼저 학습 셋과 세트스 셋을 분리한 다음에 적용을 해야 한다
         • 그렇지 않으면 학습 셋과 테스트 셋에 동일한 데이터가 들어가서 과적합을 유할하기 때문이다
         • 학습된 모델의 예측력을 검증할 때 사용하는 테스트 셋에는 오버샘플릴을 적용하지 않은 순수한 데이터를 사용해야 한다.
           • 오버샘플링이나 언더샘플링을 적용했을 때는 그렇제 않은 경우보다 예측 성능의 편차가 증가한다 → 오버샘플링이나 언더샘플링을 적용했을 때는 모델 성능 지표를 확인할 때, 여러 번 테스트를 하여 표준편차와 같은 평가 측도의 변동에 대한 정보를 같이 표기하는 것이 좋다.
     • 설정된 알고리즘 seed 값에 따라 데이터의 값이 변해서

데이타 거리 측정 방법

• 데이터 거리 측정이란?
  • 어떤 관측치를 기준으로 다른 관측치 중 어느 관측치가 더 가까이 있는가를 판단하는 것 → 데이터 유사도(similarity) 측정이라고도 함
    • 군집모델에 필수적으로 활용
  • 데이터 거리를 측정하기 전에 데이터 표준화나 정규화 가공을 해줘야 한다

대표적인 거리 측정 방법

유클리드 거리 (Euclidean distance)

• 피타고라스 정리를 활용하는 기법 → 관측치 간의 직선거리를 측정하는 것 \(d(A, B) = \sqrt{(a_1-b_1)^2 + (a_2-b_2)^2 + \text{...} + (a_n-b_n)^2} = \sqrt{\sum^{n}_{i=1}{(a_i - b_i)^2}}\)

맨해튼 거리

• 택시 거리라고도 함
• 체계적인 도시계획으로 구성된 맨해튼의 격자 모양 도로에서 최단거리를 구하는 원리를 이용한다
• 딥러닝 분야에서 정규화할 때 데이터(벡터) 간 거리를 구함
  • 맨해튼 거리 → L1
  • 유클리드 거리 → L2 \(d(A,B)= |a_1 - b_1| + |a_2 - b_2| + \text{...}+ |a_n - b_n| = \sum^{n}_{i=1}{|a_i-b_i|}\)

    민코프스키 거리

• 옵견값을 설정하여 거리 기준을 조정할 수 있는 거리 측정 방법 \(d(A,B) = (\sum^{n}_{i=1}{|a_1-b_1|^p})^{\frac{1}{p}}\)
• p값을 1로 설정하면 맨해튼 거리와 동일하고, 2로 설정하면 유클리드 거리와 동일하다

체비쇼프 거리

• 혹은 맥시멈 거리 → L max Norm으로도 부름
• 군집 간의 최대 거리를 구할 때 사용함 \(d(A,B) = max(|a_1 - b_1|) = \lim_{n → \inf}[{\sum^p_{i=1}{(a_i-b_i)^n}]^{\frac{1}{n}}}\)

  마하라노비스 거리

• X와 Y의 공분산을 고려하여 거리를 측정한다 \(d(A,B)=\sqrt{(A-B)^{\sum^{-1}}(A-B)^T}\)
• $\sum^{-1}$은 공분산 행렬이고 T는 변환행렬이다

코사인 거리

• 두 벡터의 사이각을 구해서 유사도를 구하는 것 \(\cos{\theta} = \frac{A\cdot B}{||A||||B||} = \frac{\sum^n_{i=1}{A_i \times B_i}}{\sqrt{\sum^n_{i=1}{(A_i)^2}\times \sum^n_{i=1}{(B_i)^2}}}\)