Post

데이터 분석1-1: 데이터 시각화

Posted Updated
By Nur Alya Dania binti Moriazi 20 min read

데이터 탐색과 시각화

  • 탐색적 분석, 상관성 분석과 시각화하는 단계
  • ML 모델의 성능에는 알고리즘의 우수성이나 파라미터 최적화보다 데이터를 잘 파악하고 효과적으로 가공하는 것이 더 많은 영향을 미친다.

Garbage In, Garbage Out (GIGO)란?

  • 의미가 없는 잘못된 데이터를 사용하면 역시 무의미한 결과가 나온다는 의미
  • 원천 데이터가 수많은 오류와 이상치를 가져 있을 수도 있으니 데이터를 탐색하고 시각화하여 유의미한 데이터로 정제하여 나가야 한다.

시각화

  • 분석 결과를 커뮤니케이션을 하기 위해
  • 데이터를 파악을 좀 더 효율적으로 하기 위해

탐색적 데이터 분석 (EDA)

  • 가공하지 않은 원천 데이터를 있는 그대로 탐색하고 분석하는 기법
  • 기술통계와 데이터 시각화를 통해 데이터의 특성을 파악하는 것
  • EDA를 할 때는 극단적인 해석은 피해야 하며 지나친 추론이나 자의적 해석도 지양해야 한다
  • 목적:
    • 데이터의 형태와 척도가 분석에 알맞게 되어있는지 확인 (sanity checking)
    • 데이터의 평균, 분산, 분포, 패턴 등의 확인을 통해 데이터 특성 파악
    • 데이터의 결측값이나 이상치 파악 및 보완
    • 변수 간의 관계성 파악
    • 분석 목적과 방향성 점검 및 보정

엑셀을 활용한 EDA

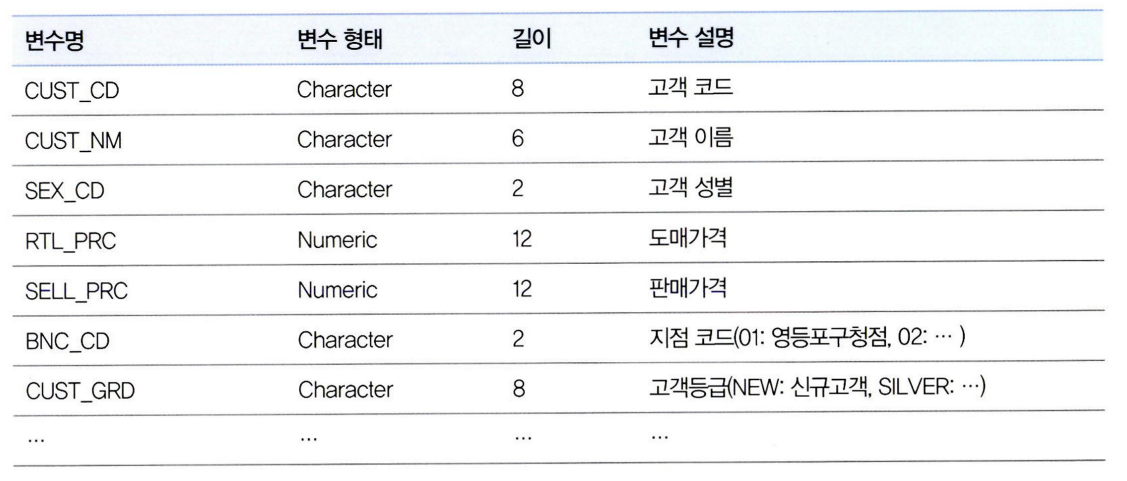
  • 각 데이터 샘플을 1000개씩 뽑아서 엑셀에 붙여 놓고 변수와 설명 리스트와 함께 눈으로 쭉 살펴보기는 EDA를 하는 가장 간단하면서 효과적인 방법이다.
    • 1000개의 행을 추출하여 변수 정의를 확인한 다음 변수 하나씩 눈으로 쭉 읽어보는 것
    • 예시: photo 1
    • 다른 데이터 가공 및 시각화 기능이 아무리 좋다 하더라도 적은 데이터를 다룰 때는 엑실만큼 사용자 친화적이고 효율적인 프로그램이 없다.

      탐색적 데이터 분석 실습

  • 판다스 info() 함수를 이용하여 데이터에 대한 전반적인 정보를 나타낼 수 있다.
    • 즉 결측값이 있는지, 데이터를 구성하는 행과 열의 크기, 각 칼럼을 구성하는 값의 자료형 등을 확인할 수 있다.
      1

        df.info()
  • 판다스 describe() 함수를 이용하여 평균, 표준편차, 최대 최솟값 등을 확인할 수 있다.
    1

      df.describe()
  • 판다스 skew() 함수와 kurtosis() 한수를 이용하여 각 칼럼의 각 왜도와 첨도를 확인할 수 있다.
    1
2

      df.skew() # 왜도 확인
  df.kurtosis() # 첨도 확인
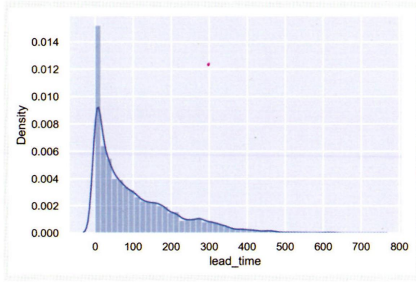
  • seaborn의 distplot() 함수로 한 칼럼의 분포를 확인하여 시각화할 수 있다.
    1

      sns.distplot(df['lead_time'])

    photo 2

  • violinplot() 함수를 이용하여 분포를 효과적으로 표현할 수 있고 stripplot() 함수로 각 관측치의 위치를 직관적으로 표현할 수 있다.
    1
2
3

      # violin plot과 strip plot 함께 그리기
  sns.violinplot(x='hotel', y='lead_time', data=df, inner=None, color='.8')
  sns.stripplot(x='hotel', y='lead_time', data=df, size=1)

    photo 3

공부산과 상관성 분석

  • 상관관계란: 타깃 변수 Y와 입력변수 X들 간의 관계
    • 독립 변수의 변화에 따른 종속 변수의 변화량을 크게 하여 통계적 정확도를 감소시키는 다중공선성을 방지할 수 있으며 데이터에 대한 이해도를 높일 수 있다.
    • 변수 간의 상관관계를 파악하는 대표적인 개념은 공부산과 상관계수이다.
      • 두 개념들은 각 변수의 변동이 얼마나 닮았는지를 표현한다는 점에 같지만 차이점도 있다.

        공부산

  • 서로 공유하는 분산을 나타내는 것
    • 즉 두 분산의 관계다

    • 공부산 계산 방식:

      \[Cov(X_{1}, X_{2}) = \sum{\frac{(\text{각 } X_1 \text{의 편차})(\text{각 } X_2 \text{의 편차})}{n(-1)}} = \frac{1}{n(-1)}\sum{(X_{1i}-\bar{x}_{1})(X_{2i}-\bar{x}_{2})}\]
      • $\text{편차} = \text{해당 값} - \text{편균}$
      • 행렬로도 계산하여 표현할 수 있다.
        • $Cov = X^TX$ photo 4 photo 5
          • 여기서 $dot(X_n, X_n)$은 분산이고 $dot(X_i, X_j)$는 공분산이다.
    • 공분산 값:
      • 0에 가까워지면 무 상관관계다
      • -1에 가까워지면 음의 상관관계다 (즉 반비례하다)
      • 1에 가까워지면 양의 상관관계다 (즉 비례하다)
      • 절댓값은 1이면 완벽한 직선의 관계다
  • 문제점: 각 변수 간의 다른 척도기준이 그대로 반영되어 공분산 값이 지니는 크기가 상관성의 정도를 나타내지 못한다.
    • 공분산을 변수 각각의 표준편차 값으로 나누는 정규화를 하여 상관성을 비교할 수 있기도 하는데 절대적인 기준이 될 수 없으므로 피어슨 상관계수를 이용하여 해결할 수 있다.

      상관계수

  • 변수 $X_1 \text{과 } X_2$가 함께 변하는 정도(공부산)를 $X_1 \text{과 } X_2$가 변하는 전체 정도로 나눠주는 것
    • 즉 $P(X_1, X_2) = \frac{Cov(X_1, X_2)}{\sqrt{Var(X_1)Var(X_2)}}, \quad (-1 \leq R \leq 1)$

| 범위(절댓값) | 단계 | | ——— | ——– | | 0 | 무 상관관계 | | 0.1 ~ 0.3 | 약 상관관계 | | 0.4 ~ 0.6 | 중 상관관계 | | 0.7 ~ 0.9 | 높은 상관관계 | | 1 | 완벽한 상관관계 |

  • 산점도로 표현해 보면: photo 6
    • 주의: 산점도의 기울기와 상관계수는 관련이 없다.
      • 분산의 관계성이 같다면 기울기가 크든 작든 상관계수는 같다.
  • 결정계수란: 상관계수를 제곱한 값
    • 해당 독립 변수가 종속변수의 변동을 설명하는 정도이다.
    • 회귀분석의 정확도를 가늠하는 기준이다.
  • 또 다른 상관분석 방법: photo 7

공분산과 상관성 분석 실습

  • seaborn의 pairplot() 함수를 이용하여 상관관계를 표현하는 산점도를 그릴 수 있다
    1

      sns.pairplot(df, diag_kind='kde') # diag_kind='kde': 상관계수가 1이면 분포로 표시
  • cov() 함수, corr() 함수로 공분산, 상관계수를 산출할 수 있다.
    1
2

      df.cov() # 공분산 확인
  df.corr(method='pearson') # 피어슨 상관계수 확인
  • heatmap() 함수로 상관계수를 이용한 히트맵을 시각화할 수 있다.
    1

      sns.heatmap(df.corr())
  • clustermap() 함수를 이용하여 기준 히트맵에 상관성이 강한 변수들끼리 묶어서 표현할 수 있다.
    1

      sns.clustermap(df.corr(), annot=True, cmap='RdYlBu_r', vmin=-1, vmax=1)

시간 시각화

  • 시계열이란: 시간 요소가 있는 데이터를 표현하는 방법
  • 선그래프 형태인 연속형과 막대그래프 형태인 분절형으로 구분할 수 있다.
    • 시간 간격의 밀도가 높은 경우: 선그래프를 사용함
      • 데이터의 양이 너무 많거나 변동이 심하면 트랜드나 패턴을 확인 어렵다.
        • 추세선을 삽입하여 들쭉날쭉한 데이터 흐름을 안정된 선으로 표현할 수 있기를 통하여 전체적인 경항이나 패턴을 쉽게 파악할 수 있다.
        • 추세선을 그리는 대표적인 방법은 이동평균(Moving average) 방법인데 이는 데이터의 연속적 그룹의 평균을 구하는 것이다.
    • 분절형시간 시각화의 경우: 막대그래프, 누적 막대그래프, 점 그래프 등 사용함
      • 예시: 월 간격으로 표현, 년별로 표현 등
      • 누적 막대그래프는 한 시점에 2개 이상의 세부 항목이 존재할 때 사용한다.

시간 시각화 실습

  • groupby() 함수를 이용하여 어떤 간격의 데이터를 가공해 줄 수 있다.
    1

      df.groupby('Date')['Sales'].sum()
  • rolling() 함수를 이용하여 어떤 간격의 이동평균선을 삽입할 수 있다.
    1

      df['Month'] = df['Sales'].rolling(window=30).mean()
  • plot.bar() 함수를 이용하여 막대그래프를 그릴 수 있고 stacked 매개변수가 True로 조절하면 누적 막대그래프를 그릴 수 있다.
    1
2
3
4
5

      ax = df.plot.bar(x='Year', y='Sales', rot=0, figsize=(10,5))

  df_bar_2_pv = df.pivot(index='Year', columns='Segment', values='Sales').reset_index()

  df_bar_2_pv.plot.bar(x='Year', stacked=True, figsize=(10,7))

비교 시각화

  • 그룹별 차이를 나타내기 위함이다
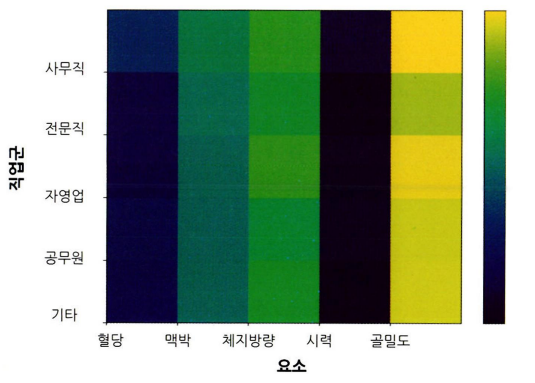
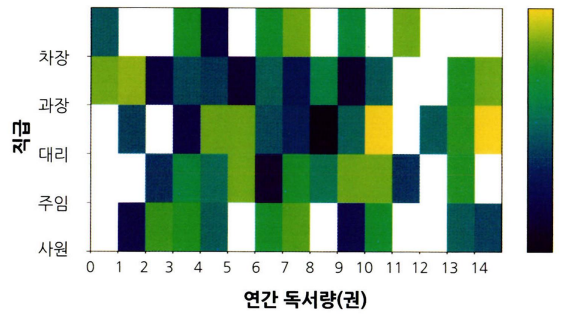
  • 그룹과 비교 요소 많을 때 효과적으로 시각화를 할 수 있는 방법은 히트맵 차트다.
  • 히트맵 차트의 표현 방법
    • 하나의 변수 (그룹) $\times$ N개의 각 변수에 해당하는 값들(수치형) photo 8
    • 하나의 변수(그룹) $\times$ 하나의 변수(그룹/수준) $\times$ 하나의 변수(수준) photo 9
    • 분류 그룹이나 변수가 너무 많으면 혼란을 유발할 수 있어서 적정한 수준으로 데이터를 정제하는 작업이 필요하다.
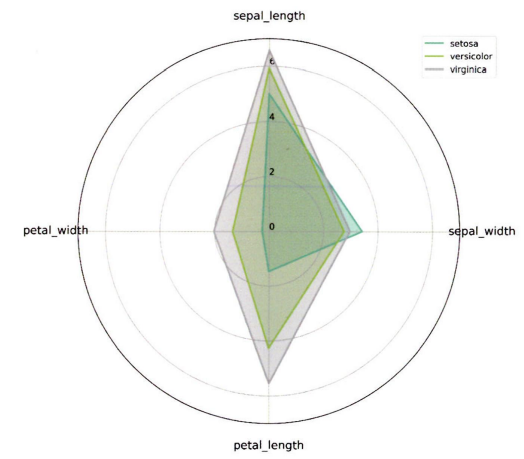
  • 또 다른 방법은 방사형 차트가 있다.
    • 하나의 차트에 하나의 그룹을 시각화 photo 10
    • 하나의 차트에 모든 그룹을 한 번에 시각 photo 11
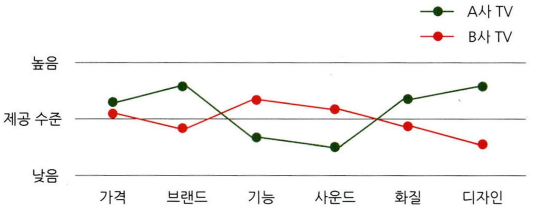
  • 평행 좌표 그래프를 통한 그룹별 요소 비교 시각화도 있다. photo 12
    • 평행 좌표 그래프를 보다 효과적으로 표현하려면 변수별 값을 정규화하면 된다.
      • 가장 낮은 값은 0%로, 가장 높은 100%로 변환하여 차이를 더욱 부각시키는 것이다.

분포 시각화

  • 연속형과 같은 양적 척도인지, 명목형과 같은 질적 척도인지에 따라 구분해서 그린다.
  • 양적 척도의 경우: 막대그래프나 선그래프로 분포를 나타낼 수도 있고 히스토그램을 통하여 분표를 단순화하여 보다 알아볼 수 있다.
  • 질적 척도로 이루어진 변수는 구성이 단순한 경우: 파이차트나 도넛차트를 사용함
  • 구성 요소가 복잡한 질적 척도를 표현하는 경우: 트리맵 차느
    • 하나의 큰 사각형을 구성 요소의 비율에 따라 작은 사각형으로 쪼개어 분포를 표현한다
    • 와플 차트는 와플처럼 일정한 네모난 조각들로 분포를 표현한다.
      • 단점: 트리맵 차트처럼 위계구조를 표현하지는 못한다.

관계 시각화

  • 산점도 그래프에 점들의 분포와 추세를 통해 두 변수 간의 관계를 파악할 수 있다.
    • 극단치로 인하여 주요 분포 구간이 압축되어 시각화의 효율이 떨어지므로 산점도를 그릴 때는 극단치를 제거하고서 그리는 것 좋다.
    • 단점: 두 개의 변수 간 관계만 표현할 수 있다
    • 해결: 버블차트
      • 3 가지 요소를 가능하고 그 이상의 요소도 가능하긴 하지만 정보가 너무 많아져 차트를 해석 어려워질 수 있다.
      • 주의: 버블차트 해석할 때는 원의 지름이 아닌 면적을 통해 크기를 판단하도록 주의해야 한다.
        • 지름이 두 배가 크면 실제 크기는 네 배가 큰 것이라서

공간 시각화

  • 위치 정보인 위도와 경도 데이터를 지도에 매핑하여 시각적으로 표현하는 것
    • 그런데 위도와 경고 정보가 없어도 지도에 위치를 표현이 가능하기도 하다.
    • 인터랙티브 한 활용이 가능하는 점을 최대한 활용하여 정보를 효과적으로 전달할 수 있도록 거시적에서 미시적으로 진행되는 분석 방향과 같이 스토리라인을 잡고 시각화를 적용하는 것이 좋다.
  • 공간 시각화 기법:

    1. 도트맵

      photo 13

      • 지리적 위치에 동일한 크기의 작은 점을 찍어서 해당 지역의 데이터 분포나 패턴을 표현하는 기법

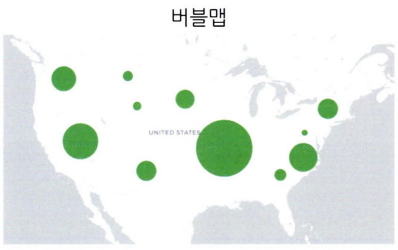
    2. 버블맵

      photo 14

      • 버블차트를 지도에 그대로 욺겨 둔 것
      • 데이터 값이 원의 크기로 표현되어 코로플래스맵보다 비울을 비교하는 것이 효과적이다.

    3. 코로플래스맵

      photo 15

      • 단계 구분도
      • 데이터 값의 크기에 따라 색상의 음영을 달리하여 해당 지역에 대한 값을 시각화하는 기법
      • 정확한 수치를 인지하고 비교하는 것이 어렵다

    4. 커넥션맵 (혹은 링크맵)

      photo 16

      • 지도에 찍힌 점들을 곡선 또는 직선으로 연결하여 지리적 관계를 표현한다.
      • 연속적 연결을 통해 지도에 경로를 표현할 수도 있다.
      • 연결선의 분포와 집중도를 통해 지리적 관계의 패턴을 파악하기 위하여 사용한다.

박스 플롯

  • 상자 수염 그림으로도 부른다.
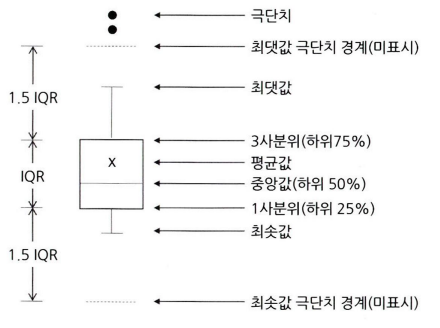
  • 박스 플롯은 네모 상자 모양에 최댓값과 최솟값을 나타내는 선이 결합된 모양의 데이터 시각화 방법이다
  • 하나의 그림으로 양적 척도 데이터의 분포 및 편행성, 평균과 중앙값 등 다양한 수치를 보기 쉽게 정리해 준다.
  • 데이터의 대체적인 분포 형태를 쉽게 확인하기 위하여 사용함
  • 카테고리별 분포를 비교할 때도 유용하게 사용된다.

  • 각 최솟값과 최댓값의 법위를 넘어가는값은 이상치로서 작은 원으로 표시한다.

    photo 17

  • 범위 계산하는 방법:

    \[\begin{aligned} Q^1 = \frac{1}{4}(n-1)\text{th value}\\ Q^2 = \frac{2}{4}(n-1)\text{th value}\\ Q^3 = \frac{3}{4}(n-1)\text{th value} \end{aligned}\]
  • 데이터의 분포를 정형화시켜 정보를 축약한 것이다.

    • 2 변수의 박스 플롯을 나란히 놓고 비교하면 각 변수 분포의 차이를 효과젹으로 비교할 수 있다.

      photo 18

  • 박스 플롯을 해석할 때는 항상 데이터 분포도를 함께 떠울리는 습관이 필요하다.

참고문헌: 데이터 분석가가 반드시 알아야 할 모든 것 10장

Study, Data Science
KHUDA ML DA
This post is licensed under CC BY 4.0 by the author.

Trending Tags

KHUDA ML DA