데이터분석 5: 신경망 + 모델 평가

신경망 + 모델 평가

인공 신경망(CNN, RNN, LSTM)

• 신경망은 복잡한 비선형적 관계를 병력적으로 분석하고 처리하고 오류나 잡음에 강하기 때에 일반화 성능이 뛰어난다

딥러닝이란

신경망 모델 구조를 확장하여 일반 기계학습 알고리즘을 뛰어넘는 정확도를 자랑하며, 이미자 인식, 문장 번역 등 다양한 분야에서 쓰이고 있다

신경망이란

• 생명체의 신경계를 이루는 신경 세포인 뉴런을 모티브로 만들어진 기계학습 모델
  • 뉴런은 수상돌기(Dendrite)들을 통해 전기적 힌호를 받는다 → 신경망 모델의 독립변수 가중 합 입력 부분
  • 입력된 전기 신호들은 세포체(soma)로 모여 합산된다 → 신경망 모델은 각 독립변수들에 가중치를 부여하여 값을 합산
  • 합산된 신호는 축삭돌기(Axon)를 통해 출력되고 생명체가 이에 반응 → 신경망 모델에서 결괏값 Y가 출력된다
• 구조:
  • 입력층: 독립변수의 값들을 입력하는 역할을 한다 → 독립변수의 수만큼 노드를 갖게 된다
  • 은닉층: 입력층에서 들어온 값들을 합산하여 보관을 하고, 노드들을 연결하는 층 사이에는 가중치들이 있다
    • 신경망 알고리즘 사이에 있어서 어떤 계산들이 이루어지는지 파악하기 힘들다 → 블랙박스 모형이라고도 함
  • 출력층: 아웃풋 출력

은닉층

• 은닉층 있는 것이 회귀분석과의 가장 큰 차이점이다
• 출력값과 Y 값과의 차이를 봐서 은닉층의 가중치를 조절한다는 차이가 있다
• 오류 역전파: 처음 주어진 가중치를 이용해 출력층의 값을 계산 → 결괏값의 오차를 각 가중치로 미분한 값을 처음 가중치에서 빼 주는 작업을 반복한다 → 가중치를 조정
• 은닉층이 2개 이상 → 딥러닝

퍼셉트론

• 입력층의 각 독립변숫값들을 하나로 합산할 때 각각에 가중치를 적용해서 보다 유의한 변수의 영향력을 강화한다 → 합산된 값이 정해진 임곗값을 초과했을 때는 1을 출력하고 못했을 때 0을 출력
• 신경망은 여러 층의 퍼셉트론으로 구성된다 → 다층 퍼셉트론(MLP: Multi-layer Perceptron)
  • 비선형 분류가 가능한다 → 과적합을 방지 가능
• 단층 퍼셉트론의 경우 AND, NAND, OR 게이트 논리 연산 가능, XOR 게이트 연산 불가능

신경망 기법

• 초기 신경망 모델은 지역 최솟값 문제가 발생 가능 → ReLU나 Drop-out 기법 등의 기법으로 해결
• 과적합 → Initialise point 사전 훈련 알고리즘 등 다양한 신경망 관련 기법
• 대표 알고리즘: CNN, RNN, LSTM

CNN

• 합성곱 신경망 (CNN: Convolution Neural Network) 사람의 시신경 구조를 모방한 구로로써 데이터의 특징을 추출하여 패턴을 파악
• 은닉층이 늘어나면 학습에 필요한 연산량은 매우 커지게 된다 → CNN은 Convolution과 Pooling 단계를 통해 해결 → 데이터를 효율적으로 연산
• Convolution이란: 합성곱의 정의는 두 함수 f, g 가운데 하나의 함수를 반점(reverse), 전이(shift)시킨 다음, 다른 하나의 함수와 곱한 결과를 적분하는 것
• Pooling이란: 설정된 영역 중에서 가장 큰 값이나 평균값 등을 추출한다
  • 방법: Max-pooling, Average-pooling, L2-norm pooling 등 → CNN에서 Max-pooling을 사용

RNN과 LSTM

순환신경망 (RNN: Recurrent Neural Network)

• 알고리즘 내부에 순환구조가 글어 있는 것 → 자연어처리 영역에서 많이 쓰이고 있다
• 출력 결과가 이전 계산 결과의 영양을 받는다는 가정으로 출발했다 → 이전의 연산 결과 정보를 갖고서 다음 연산을 순차적으로 진행하는 것
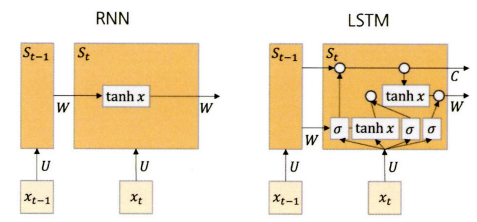
• RNN 기본 구조: - 인풋 x가 입력 → 퍼셉트론 안에서 계산된 파라미터 값이 다시 퍼셉트론 안으로 돌아가는 순환 구조를 보인다 → 결과값 출력
• 시차 요소가 척용되는 모델이라고 했다
• 각 은닉층 단위 S는 X를 입력받는다 → 기억정보를 다음 시차의 S로 전달 → S는 새로 입력받는 S값을 종합 → S로 전달 → 전갈 과정이 끝난 후 요약된 정보를 바탕으로 최종 결과를 출력
  • 은닉층: 기억을 담당
  • RNN을 사용하는 분석 주제에 따라 입출력 구조는 달라질 수 있다
• RNN 문제점: 과거 시점의 인풋과 현재 시점의 인풋과의 거리 멀면 초기의 가중치 값이 유지되지 않아 학습능력이 저하된다 → LSTM을 통해 해결

Long Short Term Memory Networks (LSTM)

• 기존 RNN과 유사한 구조를 가지고 있지만 셀 스테이트라는 요소를 가지고 있는 것
  • 셀 스테이트: 가중치를 계속 기억할 것인지 말 것인지를 결정해주는 역할을 한다 → 가중치가 기억되면 거리가 먼 과거의 인풋이라 해도 가중치가 그대로 적용된다

RNN vs LSTM

• RNN은 일반적으로 하이퍼볼릭 탄젠트 함수를 통해 전 시점의 가중치를 -1~1 사이 값으로 산출해 다음 시점에 전달 → 시그모이드 함수와 유사 → 시그모이드보다 미분 최댓값이 상대적으로 크기 때문에 가중치를 더 오래 유지할 수 있다
  • $\tanh{x} = \frac{\sinh{x}}{\cosh{x}} = \frac{e^x - e^{-x}}{e^x + e^{-x}}$
  • 결국 시차가 지날수록 과거의 가중치는 희석되어 가므로, 영향력이 급격히 줄어든다
  • 더 이상 가중치가 필요 없어도 유지된다
• LSTM은 은닉층에서 $x_{t-1}$ 시점의 가중치를 그대로 넣을 것인지 시그모이드 함수로 0, 1 사이 값으로 산출해 판단 → 결괏값에 따라 가중치를 유지할지 삭제할지 결정 → 하이퍼볼릭 탄젠트 함수를 통해 -1~1 사이 값으로 산출된다
  • 1: 가중치를 완전히 유지
  • 0: 삭제

모델 평가

학습 셋, 검증 셋, 테스트 셋과 과적합 해결

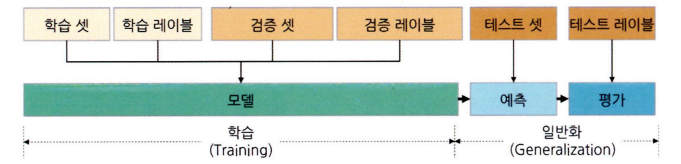
• 모델을 만들 때 데이터셋을 학습 셋, 검증 셋, 테스트 셋으로 나눠서 검증 과정을 거친다.

  학습 셋

• 모델을 학습하여 파라미터 값을 산출하기 위해 사용하는 데이터 → 모델을 학습하게 되고 가지고 있는 Y값을 잘 예측할 수 있도록 파라미터 값이 업데이트된다.
• 과적합: 학습 셋에 과도하게 적합하도록 학습되는 것 → 학습이 너무 많이 이루어지거나 변수가 너무 복잡해서 발생, train 데이터와 test 데이터가 중복될 경우에도 발생
• 과소적합: 학습이 너무 덜 되는 것

  검증 셋

• 학습 셋 데이터를 통해 모델을 만들 때 과고하게 학습되지 않도록 조정을 해주는 것
• 모델 학습 시에 검증 셋 데이터의 오차율이 더 이상 줄어들지 않고 오히려 늘어나는 시점에서 학습을 중단한다
  • 검증 셋 데이터는 학습 셋 데이터의 모델 학습 과정에 관하여 모델의 과적합을 방지해 주는 것

    테스트 셋

• 검증 셋도 결국 모델을 만들 때 관여를 한 데이터이다 → 모델 성능 지표가 다소 과장되어 있다 → 테스트 셋은 학습 셋과 검증 셋으로 만든 최종 모델의 실제 ‘최종 성능’을 평가할 때 사용
• 모델 산출시에 사용되지 않았던 테스트 셋 데이터를 통하여 실제적인 모델의 종확도를 판단하는 것

활용

• 정답지 있는 학습 셋과 검증셋으로 모델을 만들고, 모델을 테스트 셋 데이터에 적용하여 산출한 예측값을 테스트 셋 레이블과 비교하여 모델 성능을 평가 → 홀드아웃: 과적합을 방지하는 가장 기본적인 데이터셋 분리 방법
  • 반복 학습을 많이 하지 않는 간단 모델에는 검증 셋 사용을 생략하고 바로 테스트 셋에 모델을 적용하여 과적합을 검증
  • 반복 횟수가 100회 이상으로 많은 모델을 만들 때에는 앞의 인공 신경망 절의 실습에서 사용했던 model.fit(..., validation_data=(x_test, y_test))와 같이 검증 셋을 설정해 준다
• 과적합을 방지하는 방법:
  • 학습 데이터 확보
  • 결측값 처리 및 이상치 제거
  • 유의도가 낮은 변수 제거 및 차원 축소
  • 정규화(Regularisation) 적용
  • 드롭아웃 적용

Regularisation

• 모델 내주의 계수인 $\theta$ 값에 페널티를 주어 변수의 영향력을 감소시키는 기법
• 과적합된 모델의 각 가중치를 줄여 줌으로써 예측에 불필요한 변수의 영향을 최소화한다

드롭아웃

• 최종 결괏값을 계산하기 위해서 사용되는 뉴런들 중 일부를 누락(dropout)시켜 과적합을 방지하는 기법 → 신경망 모델에서 사용
• 은닉층에 드롭아웃 확률 p를 설정하면, p의 확률로 은닉층의 뉴런들이 제회된다
• 일부 뉴런이 제거된 여러 개의 모델의 결괏값을 앙상블 하기 때문에 예측 성능이 향상된다.

주요 교차 검증 방법

• 홀드아웃 방법으로 만든 모델은 결국 전체 중 일부인 검증 셋의 데이터로만 적정 학습 수준을 결정한 모델이다 → 과적합을 완전히 방지했다고 할 수 없음
  • 기존의 학습 셋과 검증 셋을 단순히 쪼개서 학습하는 방식은 모든 학습 셋 데이터를 학습에 이용할 수 없고, 데이터를 분리할 때 편향이 큰 데이터들이 한쪽에 몰리는 경우에 올바른 학습과 검증이 이루어질 수 없다는 단점 있다 → 교차검증으로 해결

K-Fold Cross Validation

• 전체 학습 데이터 중 일부를 검증 셋으로 분리하는 과정을 k 번 반복하는 방법
• 전체 학습 셋을 k 개의 조각(fold)으로 분리 → 하나의 데이터 조각을 검증 셋으로 활용하고 나머지 조각을 학습 셋으로 화용하여 모델을 학습하기 → 학습 셋으로 사용했던 데이터 조각 중 하나를 검증 셋으로 바꾸고, 방금 검증 셋으로 사용한 데이터는 다시 학습 셋에 포함시켜 학습 → 모든 분할 조합의 평균 계숫값을 구하거나 최고 성능의 모델을 선택하고 테스트 셋을 통해 최종 예측력을 평가
• 일반적으로 k의 수는 5~10개를 지정
  • k가 클수록 평가의 편중된 정도는 낮아지만, 각 fold의 모델별 결과의 분산이 높을 수 있으므로 k가 무조건 크다고 좋은 것은 아님
  • k의 수만큼 모델을 만들어야 하기 때문에, 일반 홀드아웃 방식보다 연량이 훨씬 많다는 단점이 있다

    Leave-One-Out Cross Validation(LOOCV)

• 기존 k-fold 방식에서 k를 최대화한 방법 → k를 전체 관측치 수로 하여, 검증 셋이 관측치 하나하나가 되는 것
  • 예를 들어: 전체 관측치가 1000개인 테스트 셋이면 k가 1000인 k-fold 교차검증을 수행
  • 모델의 편중이 매주 작지만 결괏값의 분산이 다소 크다는 단점이 있다 → 과적합 될 여지가 있는 방법
  • 관측치의 숫자만큼 모데를 생성하여 최종 계수를 산출하기 때문에 데이터양이 많은 경우에는 적합하지 않은 방법

    Stratified K-Fold Cross Validation

• 기존 k-fold 방식에 층화 추출 방식을 접목한 방법 → 데이터의 특정 클래스가 한 곳에 몰리는 상황을 방지할 수 있다
• 클래스 분포가 일정하지 않으면 각 부할 셋 간 계숫값의 분산이 커지게 된다 → Stratified K-Fold 교차검증은 분할 셋 안의 클래스 비율이 학습 셋 전체의 클래스 비율과 같도록 분리해 준다 → 주로 분리 모델에서 사용

  중첩 교차검증 (Nested Cross Validation)

• 기존 k-fold 방식은 학습 셋과 테스트 셋 분리를 한 번만 한다 → 모델의 성능이 테스트 셋에 크게 의존한다는 문제가 있다 → Nested CV로 해결
• 학습 셋과 테스트 셋 검증에도 k-fold 방식을 적용한 것
• k-fold를 이중으로 중첩하여 사용하므로 inner loop와 outer loop로 구성쇤다.
• Inner loop: 기존의 k-fold 교차검증과 마찬가지로 학습 셋으로 분류된 데이터를 $k-1$ 개의 테스트 셋과 1개의 검증 셋으로 나누어 k 번 학습을 수행하여 계숫값을 산출한다
• Outer loop: inner loop에서 만들어진 계숫값을 테스트 셋에 적용하여 정확도를 산출하는 작업을 k-fold 방식으로 수행한다
• 전체 데이터를 테스트 셋 데이터로 활용한다 → 만든 모델이 얼마나 잘 일반화되는지 평가하는 데 유용한 방법
• 모델의 최종 예측력 → 각 fold의 예측력 평균

  격자 탐색 교차검증 (Grid Search CV)

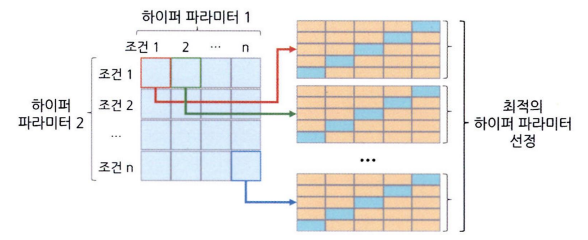
• 모델의 하이퍼파라미커 값을 리스트 형태로 미리 입력해 놓은 다음 각 조건의 모델 성능을 측정하고 평가하여 효율적으로 최적의 하이퍼파라미터 값을 찾아내는 기법
  • 파이썬 환경에서 sklearn의 GridSearchCV 패키지로 제공된다
  • 예시: 랜덤 포레스트 모델의 최대 깊이, 최소 관측치 수 등의 조건을 다양하게 지정한 후에 각 조건의 모델의 교차검증으로 평가하여 최적의 모델 조건을 찾는 것
• 종료된 후에는 최적의 하이퍼파라미터 조건과 성능을 확인할 수 있다
• 사전에 설정한 모든 하이퍼파라미터 조건의 모델을 수행 → 조건 많아지면 시간이 오래 걸린다
• 하이퍼파라미터 조건이 많은 경우 → 현실적으로 가능한 횟수 내에서 무작위로 조건을 탐색하여 최적의 조건을 찾는 무작위 탐색 방법을 사용하기도 한다.

회귀성능 평가지표

• 회귀 모델의 성능을 평가하는 주요 방법:
  • $\text{R}^2$
  • RMSE
  • MAE
  • MAPE
  • RMSLE
  • AIC
  • BIC

    R-Square와 Adjusted R-Square

• 결정계수($\text{R}^2$: R-Square)란: 회귀모델의 회귀선이 종속변수 y값을 얼마나 잘 설명할 수 있는가
• 실젯값과 예측값의 차이인 오차와, 실젯값과 실젯값과 실젯값 평균의 차이인 편차와 관려 있다
• \[\begin{aligned} \text{R}^2 = & \frac{\text{SSR}}{\text{SST}} = 1 - \frac{\text{SSE}}{\text{SST}} = \frac{\text{회귀선에 의해 설명되는 변동}}{\text{전체 변동}} \\ & \text{SSR} = \sum{(\hat{y}_i - \bar{y})^2} \\& \text{SSE} = \sum{(y_i - \hat{y}_i)^2} \\ &\text{SST} = \sum{(y_i - \bar{y})^2} = \text{SSR} + \text{SSE} \end{aligned}\]
  • Sum of Square Regression(SSR): 회귀식의 추정값과 전체 실젯값 편균과의 편차 제곱합
  • Explained Sum of Squared(SSE): 회귀식의 추정값과 실젯값 편차 제곱의 합
  • Total Sum of Squares(SST): 실젯값과 전체 실젯값 평균과의 편차 제곱합
• R-Square 값은 SSR 값이 클수록, SST 값이 작을수록 커지게 된다
  • SSR 값이 크다는 것 → 회귀선이 각 데이터를 고르게 설명한다는 의미
  • SST가 작다는 것 → SSR을 제외한 SSE가 작다는 의미
    • SSE는 실제값과 예측값의 차이 → 작을수록 모델의 설명력이 높아지는 것
• Adjusted R-Square: R-Square가 독립 변수의 개수가 많아질수록 값이 커지는 문제를 보정한 기준
  • 실제로 설명력이 전혀 없는 변수를 계속 추가하면 R-Square는 계속 증가하게 된다
  • SSE와 SST를 각각의 자유도(Degree of freedom)로 나누어 구하면 된다
  • $\text{Adj R}^2 = 1-\frac{\frac{\text{SSE}}{T-k}}{\frac{SST}{T-1}} = \frac{(n-1(1-\text{R}^2))}{(n-k-1)}$

    Root Mean Square Error (RMSE)

• 편차 제곱의 평균에 루트를 씌운 값으로, 실제 수치와 예측한 수치와의 차이를 확인하는 전형적인 방법 → 실젯값과 예측값의 표준편차를 구하는 것
• $\text{RMSE}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n{(y_i-\hat{y}_i)^2}}$
• 예측값과 실젯값의 차이가 평균적으로 어느 정도인지 측정할 수 있어 직관적으로 모델의 정확도를 가늠할 수 있다.
• 표본 평균과의 비교를 통해 대략젹인 모델 간 정확도를 비교할 수 있다
  • 표본 평균이 100이고 RMSE가 5라면, 예측값이 표본 평균 대비 5%의 변동성을 가진다고 해석
• RMSE는 예측값의 스테일에 영향에 받는다 → 종속변수의 단위가 커지면 RMSE도 커지는 것 → 모델 간 정확도 비교를 할 때 표본 데이터가 다르면 RMSE 절대치로 비교를 해서는 안된다

  Mean Absolute Error (MAE)

• 실젯값과 예측값의 차이 절댓값 합을 n으로 나눈 값 → 직관적으로 예측값 차이를 비교할 수 있다
• 오차 절댓값의 평균을 구한 것
• 두 지표 모두 예측값과 실젯값의 차이를 평균한 값이지만 계산 방식이 다르다 → 특성도 차이가 있다
• RMSE는 오차 갑슬 제곱해 준다 → MAE보다 이상치에 더 민감하다

  Mean Absolute Percentage Error (MAPE)

• 백분율 오차 → MAE를 퍼센트로 변환한 것 → 스케일에 관계없이 절대적인 차이를 비교할 수 있으므로 다른 데이터가 들어간 모델 간 성능을 비교하기에 유용하다
• 0부터 무한대의 값을 가질 수 있으며, 0에 가까울수록 우수한 모델
• $\text{MAPE}=\frac{100}{n} \sum\limits_{i=1}^n{\left\Vert \frac{\left\Vert y_i -\hat{y}_i\right\Vert}{y_i} \right\Vert}$
• MAPE 사용 시 주의할 점
  • 실젯값이 0인 경우 → 0으로 나눌 수 없기 때문에 MAPE를 구할 수 없다
    • 대부분의 분석 소프트웨어는 알아서 실젯값이 0인 관측치를 제외하고 MAPE를 계산 → 실젯값에 0이 많은 데이터는 MAPE 평가 기준을 사용하는 것이 적합하지 않다
  • 실젯값이 양수인 경우 → 실젯값보다 작은 값으로 예측하는 경우(under forecast)는 MAPE의 최댓값이 최대 100%까지만 커질 수 있다
    • 반면 실젯값보다 크게 예측하는 경우(over forecast)는 MAPE 값이 한계가 없기 때문에 MAPE 기준으로 모델을 학습하면 실젯값보다 작은 값으로 예측하도록 편향될 수 있다
  • 실젯값이 0과 가까운 매우 작은 값인 경우에 MAPE가 과도하게 높아지는 경우가 발생할 수 있다
    • 예시: 실젯값이 0.01이고 예측값이 0.05면, MAPE는 400%가 된다
    • 성능평가 방법을 선정하기 전에 실젯값과 예측값의 분포를 확인하고 이런 주의점들을 고려하여 가장 적합한 방법을 선택해야 한다

      Root Mean Square Logarithmic Error(RMSLE)

• RMSE와 동일하 수식에서 실젯값과 예측값에 1을 더해준 다음 로그를 취해준 평가 방식
• 로그를 취해 줌으로써 MAPE와 마찬가지로 상대적 비율을 비교할 수 있다
• 연유로 RMSLE는 RMSE보다 오차 이상치에 덜 민감하다 → 실젯값에 이상치가 존재하는 경우에 적당한 방식
• 로그를 취하기 전에 1을 더해주는 이유: 실젯값이 0일 때, $\log{0}$이 무한대로 수렴할 수 있다.
• $\text{RMSLE} = \sqrt{\frac{1}{n}\sum\limits_{i=1}^n{(\log{(y_i+1)}-\log{(\hat{y}_i+1)})^2}}$
• MAPE처럼 오차 비율로 모델 서응을 평가 → 스케일이 차이가 나더라도 오차 비율이 같으면 동일한 RMSLE값을 산출

  AIC와 BIC

  아카이케 정보 기준 (AIC: Akaike’s Information Criterion)

• 최대 우도(likelihood)에 독립변수가 얼마나 많은가에 따른 페널티를 반영하여 계산하는 모델 평가 척도다
  • 즉, 모델의 정확도와 함께 독립변수가 많고 적음까지 따져서 우수한 모델을 서택할 수 있도록 하는 평가 방법
• AIC 값은 작을수록 좋은 모델이며 우도가 높을 수록, 변수가 적을수록 값은 작아진다 → 변수가 늘어날수록 모델의 편의(bias)는 감소하지만 분산(variance)은 증가한다 → 적정한 변수의 개수를 찾는 데에 유용한 모델 평가 방법
• $\text{AIC} = -2 \ln{(\text{Likelihood})+2k}$
  • $-2\ln{(\text{Likelihood})}$: 모델의 적합도
  • k: 모델의 상수한을 포함한 독립변수(파라미터)의 개
    • 증가할수록 페널티를 부여하여 AIC값이 높아지게 된다
    • 그런데 AIC 방법은 데이터 수에 대한 보정은 없다 → 과늑치가 많지 않은 경우 정확도가 낮을 수 있다
    • 관측치 작은 경우: 관측치 수를 반영하여 보정된 AICc 방식을 사용 → AIC와 마찬가지로 작은 값을 가질수록 좋은 모델로 평가
      • $\text{AICc} = \text{AIC}+\frac{2k(k+1)}{n-k-1}$

        Bayes Information Criterion(BIC)

• AIC와 AICc와 유사한 개념인데 수식에서 $-2\ln{(\text{Likelihood})}$ 부분은 동일하며, 변수 개수에 대한 페널티 방식에 차이가 있다
  • $\text{BIC}=-2\ln{(\text{Likelihood})}+k\ln{(n)}$
    • 변수의 개수 $\times \ln{(n)}$으로 페널티를 부여
      • 관측치의 개수에 자연로그를 취한 값을 독립변수의 개수와 곱해준다 → 과측치가 8개 이상만 되어도 BIC가 AIC보다 변수 개수에 대한 페널티를 강하게 부여한다 → 변수의 개수를 줄이는 것을 중요하게 여기는 상황에서는 BIC로 모델을 평가하는 것이 좋다

분류, 추천 성능 평가지표

• 예측한 전체 관측치 중에서 몇 개나 정확히 분류했는가를 평가하는 것이 주요 평가 지표

  혼동 행렬

  

• 예측하게 된 관측치들이 잘 예측하기 되는지를 평가하기 위해 진양성, 위음성, 위양성, 진음성으로 나누는 개념
  • 진양성: 모델은 Positive으로 예측하고 실젯값도 동일
  • 위양성: 모델은 Positive으로 예측하고 실젯값은 상이
  • 진음성: 모델은 Negative으로 예측하고 실젯값도 동일
  • 위음성: 모델은 Negative으로 예측하고 실젯값은 상이
• 제대로 분류하지 못한 관측의 수를 전체 관측치의 수로 나눠주면 오분류를 구할 수 있다
  • 오분류율뿐 아니라 민감도, 특이도 등의 기존값을 확인하여 모델의 성능을 평가할 수 있다
  • 모델의 목적 맞춰 분류 기존값인 threshold를 조정할 수 있다

    정확도, 오분류율, 정밀도, 민감도, 특이도 그리고 f-score

• 정확도: 전체 관측치 데이터 중에서 ‘1’은 ‘1’로, ‘0’은 ‘0’으로 모델이 올바르게 분류한 비중 → 모델이 얼마나 정확하게 분류를 하는지를 나타내는 기준값이 정확도다
  • $\text{Accuracy} = \frac{\text{TP} + \text{TN}}{\text{TP}+\text{TN}+\text{FP}+\text{FN}}$
• 오분류율: 전체 관측치 데이터 중에서 모델이 잘못 분류한 비중
  • $\text{Error Rate} = \frac{\text{FP}+\text{FN}}{\text{TP}+\text{TN}+\text{FP}+\text{FN}}$
• 정밀도: ‘1’으로 예측하여 분류한 관측치 중에서 실젯값도 ‘1’인 비중
  • 모델이 실제 ‘1’을 제개로 분류하는 성능이 얼마나 우수한지를 확인할 때 정밀도 기준값을 확인
  • $\text{Precision} = \frac{\text{TP}}{\text{TP}+\text{FP}}$
• 민감도(혹은 재현율)는 실제 ‘1’인 관측치 중에서 모델이 정확히 ‘1’로 예측하여 분류한 비중
  • 모델의 정밀도가 아무리 우수하다 하더라도 실제 ‘1’인 관측치를 너무 적게 찾아낸다면 좋은 모델이라 할 수 없다
  • 비즈니스 상황에 따라 다르지만 일반적으로 50% 이상의 민감도를 유지하는 것이 좋다
  • $\text{Sensitivity} = \frac{\text{TP}}{\text{TP}+\text{FN}}$
• 특이도: ‘0’으로 예측하여 분류한 관측치 중에서 실젯값도 ‘0’인 비중
  • 보통 전체 관측치 중에서 ‘1’보다 ‘0’이 많은 비중을 차지한다 → 특이도 높게 나오는 편이다
  • $\text{Specificity}=\frac{\text{TN}}{\text{TN}+\text{FP}}$
• 정확도와 정밀도 평가 시 주의해야 할 점:
  • 상황에 따라서는 클래스 불균형을 없애기 위해 언더샘플링이나 오버샘플링 등을 통해 ‘1’과 ‘0’ 클래스의 비율을 비숫하게 맞춰 주기도 하지만 8:2 정도의 비율 그래도 분류 예측을 하기도 한다 → 정확도는 80%가 된다 → 정확성 역설
  • 모델이 단 하나의 관측치만 ‘1’로 분류했도 실젯값도 ‘1’이라면 그 모델의 정밀도는 100%가 된다
  • 위험해서 특이도, 민감도로 평가
• F-Score: 정말도와 민감도를 동시에 고려한 분류 모델 성능 평가 기준
  • 정확도와 민감도는 서로 트레이드오프 관계
    • 정확도가 증가하면 민감도 감소하고, 민감도가 증가하면 정밀도가 감소하게 된다
    • 정밀도를 높인다는 것은 실제로 ‘1’일 것이 거의 확실한 관측치만 ‘1’로 예ㅡㄱ하여 분류한다는 것 → 전체 실제 ‘1’ 중에 ‘1’로 분류되는 비우인 민감도는 감소할 수밖에 없다
    • 정밀도와 민감도 둘의 조화평균을 한 기준값을 사용하여 보다 객관적으로 분류모델을 평가할 수 있다
    • $\text{F-score} = \frac{(1+\beta^2) \times (\text{precision} \times \text{sensitivity})}{(\beta^2\times \text{precision})+\text{sensitivity}}$
      • $\beta^2$: 조화평균의 가중치 → 정밀도와 민감도의 중요도를 동일하게 본다면 $\beta$에 1에 대입해 준다
• G-mean: F-score와 유사한 개념인데 기하평균을 사용
  • 민감도와 특이도의 평균을 구한다
  • 기하평균의 특성상 더 작은 값에 가중치를 준다 → 님감도와 특이도 중 하나의 값이 확연히 떨어지면 G-mean 값은 단순 산술평균한 값보다 더 떨어지게 된다
  • $\text{G-mean} = \sqrt{\text{specificity}\times\text{sensitivity}} = \sqrt{(1-\alpha)\times(1-\beta)}$

    향상도 테이블과 향상도 차트 그리고 향상도 곡선

• 향상도 테이블과 행상도 곡선은 전체 threshold 값에 대한 모델을 평가하는 지표로 사용할 수 있다
• 적정한 threshold 값을 선정할 때에도 사용할 수 있는 유용한 모델 평가 기준

  향상도 테이블

• 향상도 테이블의 향상도란, 전체 관측치 중에서 실제 ‘1’의 비율보다, 모델을 통해 ‘1’로 예측한 관측치 중 실제 ‘1’의 비율이 얼마나 더 높은지를 나타낸다
• 향상도 테이블은 모델이 ‘1’로 분류될 확률이 높은 관측치는 길제로 ‘1’인 경우가 많다는 것을 전제로 한다.
  • 모델이 제대로 학습됐다면 ‘1’로 분류될 확률이 높을수록 실젯값과 일지할 확률이 높아야 한다
  • 만약 무작위로 ‘1’을 뽑는 확률보다 모델이 ‘1’을 분류할 확률이 낮으면 향상도는 1미만이 된다
  • 향상도 만드는 과정:
  • 향상도 테이블을 활용하여 각 분위수에 포함된 실젯값 ‘1’의 비율을 확인하여 모델 성능을 확인할 수 있다
    • 상위 분위수에 ‘1’이 많이 포함될수록 ‘1’을 더 잘 맞춘다는 의미이므로 좋은 모델이라 할 수 있다.
  • 분위수가 바뀔 때마다 향상도 값이 확연하게 줄어드는 형태가 이상적이다
    • 분류를 잘 못하는 모델은 실제 ‘1’값이 전체 분위수에 골고루 퍼져 있게 되므로 향상도 분위수마다 비숫하다 → 이를 보다 직관적으로 확인할 수 있도록 막대그래프로 표현한 것을 향상도 차트 혹은 심분위도라 부른다

      향상도 차트

• 각 분위수의 민감도 갓을 막대그래프로 표현한다
• 좋은 모델은 상위 분위수에서 높은 막대 형태를 취하다가 갑자기 줄어드는 형태를 보인다

  향상도 곡선

• 뉴적 향상도 차트는 10분위수로 띄엄띄엄 나눈다 → 세세한 threshold를 결정하기 어렵다 → 100분위수로 표현된 누적 향상도 곡선을 사용
• 기준선: 해당 분위수의 누적 관측치 수/전체 관측치수다
  • 기준선 위로 볼록하게 나온 선은 해당 분위수까지 누적된 ‘1’의 비율
  • 주의할 점: 선의 모수는 ‘1’인 관측치 전체이고, 기준선의 모수는 전체 관측치다

    ROC 곡선과 AUC

• 혼동행렬을 활용한 분류모델 평가지표 중 Receiver Operator Characteristic(ROC) 곡선과 Area Under Curve(AUC)가 있다.
  • 객관적으로 모델 비교 및 평가를 할 수 있고 임곗값인 threshold를 결정하는 데에 유용하게 사용할 수 있다는 장점이 있다

    ROC

• ROC 곡선의 접근 방식은 향상도 테이블과 유사하다
• 임곗값 threshold를 1에서 0으로 조정해 가면서 민감도와 1-특이도 값을 2차원 좌표에 찍어서 그래프를 그린다
• 민감도와 1-특이도 값의 변화를 그래프로 그려서 분류 모델의 성능을 평가하는 것
  • 좋은 모델이하면 높은 threshold 구간에 실제 ‘1’값이 많이 몰려 있고 낮은 구간에는 실제 ‘1’값이 희소할 것이다 → 좋은 모델일수록 ROC 곡선은 좌측 상단에 수렴하게 된다.

    AUC

• 곡선 그래프만으로 모델의 성능을 객관적으로 판단하기는 어렵다 → ROC 곡선을 수치로 계산한 AUC 기준을 활용한다
• ROC 곡선 아래의 면적 크기를 구한 것
  • 면젹의 크기가 클수록 유슈한 모델이며, 0.5는 랜덤 분류와 같은 성능 → AUC가 0.5이하인 모델은 무작위로 분류하는 것보다 못하다는 뜻
    • AUC가 0.5 이하로 나왔다면 데이터에 이상이 있거나, 모델링에 심각한 실수가 있지 않은지 확인해야 한다

      ROC 곡선으로 임곗값 Threshold를 선정하는 방법

• ROC 곡선의 좌표를 테이블 형태로 출력한 다음 가장 이상적인 만감도와 1-특이도 조합에 해당되는 임곗값 지점을 찾으면 된다
• ROC 곡선의 좌표 정보 데이터 분석 환경 자체에서 제공되는 경우도 있고, 직접 만들어야 하는 경우고 있다
• 암계치 구간별 민감도와 1-특이도 값 테이블은 간단한 쿼리로 구현할 수 있다.

수익 곡선

• 진양성에 따른 이익과 위양성에 따른 손해를 수치화하여 분류 모델의 수익성을 최대화할 때 사용하는 것
• 실제 비즈니스 상황에서는 예상 비용을 정확하게 예측하는 것이 불가능하며, 측정이 어려운 복합적으로 고려해야 하므로 수익곡선은 보조 지표로 활용하는 것이 좋다.
• 수익곡선을 만드는 과정은 향상도 곡선이나 ROC곡선을 만드는 방법과 유사하다
  1. 관측치들을 Predicted probability가 높은 수느로 정렬한다
  2. threshold 각 지점의 정밀도를 활용하여 기대 수익을 측정
  3. 선그래프로 표현한 다음, 다용 예산 안에서 최대의 수익을 얻을 수 있는 지점을 선택하면 된다

Precision at K, Recall at K 그리고 MAP

• 또 다른 평가 방법: Mean Average Precision(MAP)
  • 사용자들이 반응했던 항목 구간들의 Precision들을 모두 평균을 낸 모델 평가 척도
  • 많은 구간의 Precision 정보를 활용한다 → 수치가 안정적이다
  • 추천 시스템 모델 간 성능을 비교할 때는 MAP값을 비교하여 최적의 모델을 선택할 수 있다
  • k 값을 정했다면 Precision at K와 Recall at K 수치도 함께 고려하는 것이 좋다

  

A/B 테스트와 MAB

A\B 테스트

• 가장 직관적이고 확실한 성과를 측정하는 방법은 AS-IS와 TO-BE의 결과를 직접 비교하는 것
• A/B 테스트: 임의호 두 집단으로 나눠서 서로 다른 콘텐트를 보여준 다음 어떤 집단이 더 높은 성과를 보이는지를 비교한다

  A/B 테스트 주제와 절차

• A/B 테스트 진행하는 방법:

  단점

• 표본 그룹이 편향되지 않도록 무작위 추출을 올바르게 시행하여야 한다
• 표본 수는 많을수록 좋지만, 일반적으로 1000명 이상의 표본으로 테스트를 하는 것이 좋다
  • 통계적으로는 30명 이상이 되어도 유의성 검증이 가능하지만 온라인 데이터는 변화가 크고, 클릭률 같은 경우 그 비율이 매우 작은 경우가 많다 → 충분한 표본을 확보하는 겅이 좋다
• 각 집단의 반응률은 시간대, 요일 등에 차이가 있을 수 있으므로 되도록 24시간 이상 A/B 테스트를 진행해야 한다
  • 이론적으로 A/B 테스트는 일시적으로 하는 것이 아니라, 지속적으로 진행하는 것이 좋다
• A/B 테스트를 기획할 때 한 사용자가 한 가지 변화만 경험하도록 설계해야 한다
• 테스트 가능한 경우의 수는 매우 다양해서 최적의 조건을 찾을 때까지 오랜 시간과 비용이 필요하다는 것
• 기회비용이 크고, 빠른 트랜드 변화에 둔감하다는 단점이 있다 → 보완한 방법 MAB

  Multi-Armed Bandit (MAB)

  Exploration과 Exploitation

• Exploration: 최적의 보상을 얻을 수 있는 방안을 찾기 위해 계속해서 실험하는 것
• Exploitation: 선택한 최적의 방안을 계속 실행하여 이익을 최대화하는 것
• trade-off 관계-> 조합을 최적화하여 최대의 이익을 얻는 것이 MAB의 목적이다
• Multi-armed: 여러 개의 손잡이
• Bandit: 슬롯머신
• 슬롯머신의 여러 손잡이를 가장 효과적으로 사용하는 알고리즘

$\epsilon$- greedy

• 일정 확률로 대안을 무작위로 탐색하는 알고리즘
• $1-\epsilon$의 확률로 현재까지 exploration한 대안 중 가장 성과가 좋은 대안을 선택한다 → 나머지 $\epsilon$ 값의 확률로는 무작위로 대안을 선택한다
• $\epsilon$ 값이 클수록 새로운 대안을 찾기 위한 exploration 작업을 더 많이 하게 되는 것

  Upper Confidence Bound (UCB)

• 대안의 결과가 불확실한 것을 우선순위로 탐색하는 알고리즘
• $\epsilon$-greedy 알고리즘이 대안 탐색을 좀 더 스마트하게 할 수 있도록 보완한 알고리즘이다
• 기본 방식은 $\epsilon$-greedy와 마찬가지로 일정 확률로 대안을 탐색하지만, 대안을 탐색하는 방식이 보합리적이다
• 탐색을 적게 했다는 것은 그 대안의 보상이 아직 확실하지 않다는 뜻 → 더 많은 가중치를 주는 방식

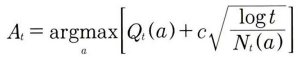
  톰손 샘플링

• 대안의 결과에 대한 베타 분휴를 계산하여 샘플링한 값 중 가장 높은 대안을 탐색하는 알고리즘
• 베타 분포를 사용하여 확률적으로 수익을 추정하고 선택하는 확률적 알고리즘
• 사전 수익률을 베타분포를 통해 다시 추정한다 → expliration을 적게 한 상황에서는 특정 대안이 수익률이 높게 나오더라도 베타 분포에 의해 추정되어 다른 대안을 선택할 수 있는 여지가 생긴다

  베타 분포

• 베르노이 분포와 같은 이항 분포인데, 베르노이 같은 경우 샘플의 결과가 모두 1이면 $\mu=1$ 이 되어 과적합이 발생
• 베이지안 방식으로 파라미터를 추정하므로 샘ㄹ플이 적더라도 안정된 추정값을 얻을 수 있다

  활용 분야

• 기계학습
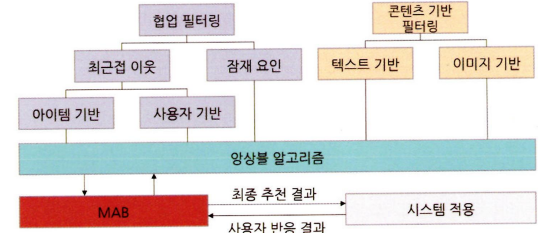
• 앙상블 방식 → 사용자의 실제 반응 정보를 바로 반영하여 실제 반응률이 가장 좋은 모델을 적용한 아이템 추천을 하여 반응률을 극대화할 수 있다